
【题目】设数组![]() ,
,![]() ,
,![]()
![]() ,数
,数![]() 称为数组
称为数组![]() 的元素.对于数组
的元素.对于数组![]() ,规定:
,规定:
①数组![]() 中所有元素的和为
中所有元素的和为![]() ;
;
②变换![]() ,
,![]() 将数组
将数组![]() 变换成数组
变换成数组![]() ,其中
,其中![]() 表示不超过
表示不超过![]() 的最大整数;
的最大整数;
③若数组![]() ,则当且仅当
,则当且仅当![]()
![]() 时,
时,![]() .
.
如果对数组![]() 中任意
中任意![]() 个元素,存在一种分法,可将其分为两组,每组
个元素,存在一种分法,可将其分为两组,每组![]() 个元素,使得两组所有元素的和相等,则称数组
个元素,使得两组所有元素的和相等,则称数组![]() 具有性质
具有性质![]() .
.
(Ⅰ)已知数组![]() ,
,![]() ,计算
,计算![]() ,
,![]() ,并写出数组
,并写出数组![]() 是否具有性质
是否具有性质![]() ;
;
(Ⅱ)已知数组![]() 具有性质
具有性质![]() ,证明:
,证明:![]() 也具有性质
也具有性质![]() ;
;
(Ⅲ)证明:数组![]() 具有性质
具有性质![]() 的充要条件是
的充要条件是![]() .
.
【答案】(Ⅰ)数组![]() 是具有性质
是具有性质![]() ,数组
,数组![]() 不具有性质
不具有性质![]() .(Ⅱ)证明见解析(Ⅲ)证明见解析
.(Ⅱ)证明见解析(Ⅲ)证明见解析
【解析】
(Ⅰ)根据题意,即可容易得![]() ,则可判断;
,则可判断;
(Ⅱ)对![]() 都为奇数和都为偶数,结合性质
都为奇数和都为偶数,结合性质![]() 的定义,即可证明;
的定义,即可证明;
(Ⅲ)从充分性和必要性上,结合(Ⅱ)中所求,即可证明.
(Ⅰ)![]() ,
,![]() ;
;
数组![]() 是具有性质
是具有性质![]() ,数组
,数组![]() 不具有性质
不具有性质![]() .
.
(Ⅱ)证明:当元素![]() 均为奇数时,
均为奇数时,
因为![]() ,
,![]() ,所以
,所以![]() .
.
对![]() 中任意
中任意![]() 个元素,不妨设为
个元素,不妨设为![]() .
.
因为数组![]() 具有性质
具有性质![]() ,所以对于
,所以对于![]() ,
,
存在一种分法:将其分为两组,每组![]() 个素,使得各组内所有元素之和相等.
个素,使得各组内所有元素之和相等.
如果用![]() 替换上述分法中的
替换上述分法中的![]() (
(![]() ),
),
就可以得到对于![]() 的一种分法:
的一种分法:
将其分为两组,每组![]() 个元素,显然各组内所有元素之和相等.
个元素,显然各组内所有元素之和相等.
所以此时![]() 也具有性质
也具有性质![]() .
.
当元素![]() 均为偶数时,
均为偶数时,
因为![]() ,
,![]() ,所以
,所以![]() .
.
对![]() 中任意
中任意![]() 个元素,不妨设为
个元素,不妨设为![]() .
.
因为数组![]() 具有性质
具有性质![]() ,所以对于
,所以对于![]() ,
,
存在一种分法:将其分为两组,每组![]() 个元素,使得各组内所有元素之和相等.
个元素,使得各组内所有元素之和相等.
如果用![]() 替换上述分法中的
替换上述分法中的![]() (
(![]() ),
),
就可以得到对于![]() 的一种分法:
的一种分法:
将其分为两组,每组![]() 个元素,显然各组内所有元素之和相等.
个元素,显然各组内所有元素之和相等.
所以此时![]() 也具有性质
也具有性质![]() .
.
综上所述,由数组![]() 具有性质
具有性质![]() 可得
可得![]() 也具有性质
也具有性质![]() .
.
(Ⅲ)证明:(1)充分性:显然成立.
(2)必要性:
因为数组![]() 具有性质
具有性质![]() ,所以对于数组
,所以对于数组![]() 中任意
中任意![]() 个元素,存在一种分法:
个元素,存在一种分法:
将![]() 个元素平均分成2组,并且各组内所有元素之和等于同一个正整数,
个元素平均分成2组,并且各组内所有元素之和等于同一个正整数,
所以![]() 均为偶数,从而元素
均为偶数,从而元素![]() 的奇偶性相同.
的奇偶性相同.
由(Ⅱ)可知,如果数组![]() 具有性质
具有性质![]() ,
,
那么![]() 仍具有性质
仍具有性质![]() .
.
又因为,当![]() 为奇数时,
为奇数时,
![]() ,当且仅当
,当且仅当![]() 时等号成立,
时等号成立,
当![]() 为偶数时,
为偶数时,
![]() ,
,
由此得到![]() 的充要条件是
的充要条件是![]() .
.
易知![]() ,
,
当且仅当![]() 时等号成立.
时等号成立.
即![]() ,当且仅当
,当且仅当![]() 时等号成立.
时等号成立.
令![]() ,
,![]() ,
,![]() .
.
假设对于任意的![]() ,有
,有![]() ,则
,则![]() ,
,
又![]() ,
,![]() ,得
,得![]() ,即
,即![]() .
.
得![]() ,…,
,…,
![]() ,
,
所以![]() ,且
,且![]() 单调递减.
单调递减.
又因为![]() ,矛盾.
,矛盾.
所以存在![]() ,有
,有![]() .
.
又由结论1,得此时![]() .
.
上述过程倒推回去,
因为数组![]() 均具有性质
均具有性质![]() ,即数组
,即数组![]() 中元素
中元素![]()
的奇偶性相同,可得数组![]() 中的所有元素都相同,
中的所有元素都相同,
所以,数组![]() 中的元素均相同,即
中的元素均相同,即![]() .
.


科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,以
中,以![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 与
与![]() 的直角坐标方程;
的直角坐标方程;
(2)若![]() 与
与![]() 的交于
的交于![]() 点,
点,![]() 与
与![]() 交于
交于![]() 、
、![]() 两点,求
两点,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年安庆市在大力推进城市环境、人文精神建设的过程中,居民生活垃圾分类逐渐形成意识.有关部门为宣传垃圾分类知识,面向该市市民进行了一次“垃圾分类知识"的网络问卷调查,每位市民仅有一次参与机会,通过抽样,得到参与问卷调查中的1000人的得分数据,其频率分布直方图如图:
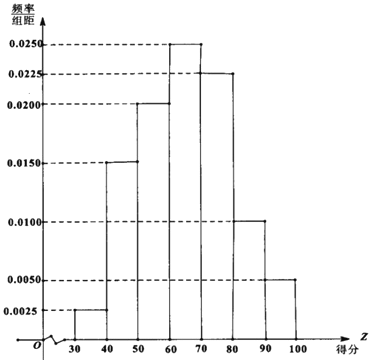
(1)由频率分布直方图可以认为,此次问卷调查的得分Z服从正态分布![]() ,
,![]() 近似为这1000人得分的平均值(同一组数据用该区间的中点值作代表),利用该正态分布,求P(
近似为这1000人得分的平均值(同一组数据用该区间的中点值作代表),利用该正态分布,求P(![]() );
);
(2)在(1)的条件下,有关部门为此次参加问卷调查的市民制定如下奖励方案:
(i)得分不低于![]() 可获赠2次随机话费,得分低于
可获赠2次随机话费,得分低于![]() 则只有1次:
则只有1次:
(ii)每次赠送的随机话费和对应概率如下:
赠送话费(单位:元) | 10 | 20 |
概率 |
|
|
现有一位市民要参加此次问卷调查,记X(单位:元)为该市民参加问卷调查获赠的话费,求X的分布列.附:![]() ,若
,若![]() ,则
,则![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】密云某商场举办春节优惠酬宾赠券活动,购买百元以上单件商品可以使用优惠劵一张,并且每天购物只能用一张优惠券.一名顾客得到三张优惠券,三张优惠券的具体优惠方式如下:
优惠券1:若标价超过50元,则付款时减免标价的10%;
优惠券2:若标价超过100元,则付款时减免20元;
优惠券3:若标价超过100元,则超过100元的部分减免18%.
如果顾客需要先用掉优惠券1,并且使用优惠券1比使用优惠券2、优惠券3减免的都多,那么你建议他购买的商品的标价可以是__________元.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】秉承“绿水青山就是金山银山”的发展理念,某市环保部门通过制定评分标准,先对本市的企业进行评估,评出四个等级,并根据等级给予相应的奖惩,如下表所示:
评估得分 |
|
|
|
|
评定等级 | 不合格 | 合格 | 良好 | 优秀 |
奖励(万元) |
|
|
|
|
环保部门对企业评估完成后,随机抽取了![]() 家企业的评估得分(
家企业的评估得分(![]() 分)为样本,得到如下频率分布表:
分)为样本,得到如下频率分布表:
评估得分 |
|
|
|
|
|
|
频率 |
|
|
|
|
|
|
其中![]() 、
、![]() 表示模糊不清的两个数字,但知道样本评估得分的平均数是
表示模糊不清的两个数字,但知道样本评估得分的平均数是![]() .
.
(1)现从样本外的数百个企业评估得分中随机抽取![]() 个,若以样本中频率为概率,求该家企业的奖励不少于
个,若以样本中频率为概率,求该家企业的奖励不少于![]() 万元的概率;
万元的概率;
(2)现从样本“不合格”、“合格”、“良好”三个等级中,按分层抽样的方法抽取![]() 家企业,再从这
家企业,再从这![]() 家企业随机抽取
家企业随机抽取![]() 家,求这两家企业所获奖励之和不少于
家,求这两家企业所获奖励之和不少于![]() 万元的概率.
万元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年末,武汉出现新型冠状病毒肺炎(![]() )疫情,并快速席卷我国其他地区,传播速度很快.因这种病毒是以前从未在人体中发现的冠状病毒新毒株,所以目前没有特异治疗方法,防控难度很大.武汉市出现疫情最早,感染人员最多,防控压力最大,武汉市从2月7日起举全市之力入户上门排查确诊的新冠肺炎患者、疑似的新冠肺炎患者、无法明确排除新冠肺炎的发热患者和与确诊患者的密切接触者等“四类”人员,强化网格化管理,不落一户、不漏一人.在排查期间,一户6口之家被确认为“与确诊患者的密切接触者”,这种情况下医护人员要对其家庭成员随机地逐一进行“核糖核酸”检测,若出现阳性,则该家庭为“感染高危户”.设该家庭每个成员检测呈阳性的概率均为
)疫情,并快速席卷我国其他地区,传播速度很快.因这种病毒是以前从未在人体中发现的冠状病毒新毒株,所以目前没有特异治疗方法,防控难度很大.武汉市出现疫情最早,感染人员最多,防控压力最大,武汉市从2月7日起举全市之力入户上门排查确诊的新冠肺炎患者、疑似的新冠肺炎患者、无法明确排除新冠肺炎的发热患者和与确诊患者的密切接触者等“四类”人员,强化网格化管理,不落一户、不漏一人.在排查期间,一户6口之家被确认为“与确诊患者的密切接触者”,这种情况下医护人员要对其家庭成员随机地逐一进行“核糖核酸”检测,若出现阳性,则该家庭为“感染高危户”.设该家庭每个成员检测呈阳性的概率均为![]() (
(![]() )且相互独立,该家庭至少检测了5个人才能确定为“感染高危户”的概率为
)且相互独立,该家庭至少检测了5个人才能确定为“感染高危户”的概率为![]() ,当
,当![]() 时,
时,![]() 最大,则
最大,则![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某健身房为了解运动健身减肥的效果,调查了![]() 名肥胖者健身前(如直方图(1)所示)后(如直方图(2)所示)的体重(单位:
名肥胖者健身前(如直方图(1)所示)后(如直方图(2)所示)的体重(单位:![]() )变化情况:
)变化情况:
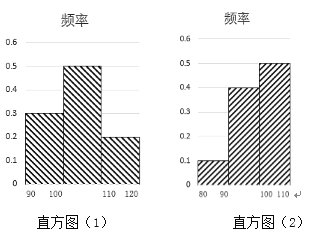
对比数据,关于这![]() 名肥胖者,下面结论正确的是( )
名肥胖者,下面结论正确的是( )
A.他们健身后,体重在区间![]() 内的人数较健身前增加了
内的人数较健身前增加了![]() 人
人
B.他们健身后,体重原在区间![]() 内的人员一定无变化
内的人员一定无变化
C.他们健身后,![]() 人的平均体重大约减少了
人的平均体重大约减少了![]()
D.他们健身后,原来体重在区间![]() 内的肥胖者体重都有减少
内的肥胖者体重都有减少
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com