练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在平面直角坐标系xOy中，曲线C的参数方程为(α为参数)，在以坐标原点O为极点，x轴的正半轴为极轴的极坐标系中，点P的极坐标为，直线l的极坐标方程为.

    (1)求直线l的直角坐标方程与曲线C的普通方程；

    (2)若Q是曲线C上的动点，M为线段PQ的中点，直线l上有两点A，B，始终满足|AB|＝4，求△MAB面积的最大值与最小值.

    【答案】（1），；（2）最大值为，最小值为.

    【解析】

    （1）由，，可将直线的方程转化为直角坐标方程，由曲线的参数方程消去参数，可得其普通方程；

    （2）设，由条件可得，再由到直线的距离求出最值即可．

    解：（1）直线的极坐标方程为，即．

    由，，可得直线的直角坐标方程为，

    将曲线的参数方程，消去参数，

    得曲线的普通方程为；

    （2）设，，

    点的极坐标化为直角坐标为，

    则，

    点到直线的距离，其中

    所以

    面积的最大值为，最小值为

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数．

    （1）证明：；

    （2）设，在上的极值点从小到大排列为，求证：时，．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某地有两个国家AAAA级景区—甲景区和乙景区.相关部门统计了这两个景区2019年1月至6月的客流量（单位：百人），得到如图所示的茎叶图.关于2019年1月至6月这两个景区的客流量，下列结论正确的是（ ）

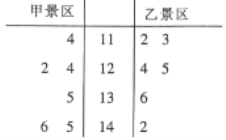
    A.甲景区客流量的中位数为13000

    B.乙景区客流量的中位数为13000

    C.甲景区客流量的平均值比乙景区客流量的平均值小

    D.甲景区客流量的极差比乙景区客流量的极差大

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列函数在其定义域上既是奇函数，又是增函数的是（ ）

    A.B.

    C.D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】给定函数、，定义.

    （1）证明：；

    （2）若，，证明：是周期函数；

    （3）若，，，，，证明：是周期函数的充要条件是为有理数.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】函数.

    （1）根据不同取值，讨论函数的奇偶性；

    （2）若，对于任意的，不等式恒成立，求实数的取值范围；

    （3）若已知，. 设函数，，存在、，使得，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】抛物线的焦点为，是抛物线上关于轴对称的两点，点是抛物线准线与轴的交点，是面积为的直角三角形.

    （1）求抛物线的方程；

    （2）点在抛物线上，是直线上不同的两点，且线段的中点都在抛物线上，试用表示.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知.

    （Ⅰ）当时,判断的奇偶性,并说明理由；

    （Ⅱ）当时,若,求的值；

    （Ⅲ）若,且对任何不等式恒成立,求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系中，曲线的参数方程为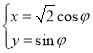（为参数），以坐标原点为极点，轴的正半轴为极轴建立极坐标系，曲线的极坐标方程为.

    （1）求曲线的极坐标方程和的直角坐标方程；

    （2）设是曲线上一点，此时参数，将射线绕原点逆时针旋转交曲线于点，记曲线的上顶点为点，求的面积.

    查看答案和解析>>

    同步练习册答案