若角α始边为x轴非负半轴.终边上一点A.则sinα等于( )A．$\frac{1}{2}$B．-$\frac{1}{2}$C．$\frac{\sqrt{3}}{2}$D．-$\frac{\sqrt{3}}{2}$ 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

8．若角α始边为x轴非负半轴，终边上一点A（1，-$\sqrt{3}$），则sinα等于（　　）

A．

$\frac{1}{2}$

B．

-$\frac{1}{2}$

C．

$\frac{\sqrt{3}}{2}$

D．

-$\frac{\sqrt{3}}{2}$

分析由题意可得x=1，y=-$\sqrt{3}$，r=2，根据sinα=$\frac{y}{r}$，即可求得结果．

解答解：由题意可得x=1，y=-$\sqrt{3}$，∴r=2，∴sinα=$\frac{y}{r}$=-$\frac{\sqrt{3}}{2}$，
故选：D．

点评本题主要考查任意角的三角函数的定义，属于基础题．

练习册系列答案

本土教辅轻松寒假总复习系列答案

高效课堂系列寒假作业系列答案

寒假生活微指导系列答案

培优教育寒假作业武汉大学出版社系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：填空题

18．已知f（x）=|log₂x|，正实数a，b满足f（a）=f（b），且a＜b，若f（x）在区间[a²，b]上的最大值为3，则a+b=$\frac{9\sqrt{2}}{4}$．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

19．

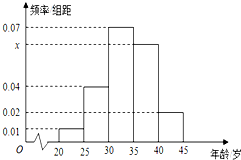为增强市民的节能环保意识，某市面向全市征召义务宣传志愿者．从符合条件的500名志愿者中随机抽取100名志愿者，其年龄频率分布直方图如图所示，其中年龄分组区间是：[20，25），[25，30），[30，35），[35，40），[40，45]．
（Ⅰ）求图中x的值并根据频率分布直方图估计这500名志愿者中年龄在[35，40）岁的人数；
（Ⅱ）在抽出的100名志愿者中按年龄采用分层抽样的方法抽取20名参加中心广场的宣传活动，再从这20名中采用简单随机抽样方法选取3名志愿者担任主要负责人．记这3名志愿者中“年龄低于35岁”的人数为X，求X的分布列及数学期望．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

16．某企业生产甲乙两种产品均需用A，B两种原料，已知生产1吨每种产品需原料及每天原料的可用限额如表所示，如果生产1吨甲、乙产品可获利润分别为3万元、4万元，则该企业每天可获得最大利润为（　　）