
 是在
是在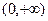 上每一点均可导的函数,若
上每一点均可导的函数,若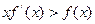 在
在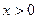 时恒成立.
时恒成立.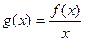 在
在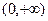 上是增函数;
上是增函数;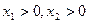 时,有
时,有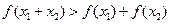 ;
; 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案科目:高中数学 来源:不详 题型:解答题
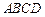 中,已知
中,已知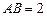 ,
,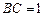 ,在
,在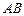 .
.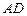 .
.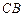 .
.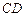 上,分别截取
上,分别截取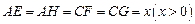 ,设四边形
,设四边形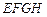 的面积为
的面积为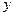 .
.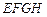 的面积
的面积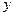 与
与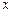 之间的函数关系式;
之间的函数关系式;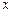 为何值时
为何值时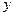 取得最大值,最大值是多少?
取得最大值,最大值是多少?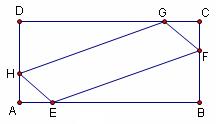
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
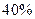 出售,根据市场调查,原价每降低
出售,根据市场调查,原价每降低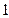 个百分点,月销售件数将增加
个百分点,月销售件数将增加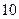 个百分点,为使月毛利润(=月销售总额-月成本总额)比原来增加幅度不小于
个百分点,为使月毛利润(=月销售总额-月成本总额)比原来增加幅度不小于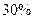 ,问降价至多多少个百分点?
,问降价至多多少个百分点?查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
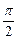 ],设M={m|g(θ)<0,m∈R},N={m|f[g(θ)]<0},求M∩N.
],设M={m|g(θ)<0,m∈R},N={m|f[g(θ)]<0},求M∩N.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com