
【题目】设集合![]() ,
, ![]() 是集合
是集合![]() 的所有子集组成的集合.若集合
的所有子集组成的集合.若集合![]() 满足对任意的映射
满足对任意的映射![]() ,总存在
,总存在![]() ,使得
,使得![]() 成立,其中,
成立,其中,![]() 表示集合
表示集合![]() 的子集
的子集![]() 的补集,
的补集,![]() 为给定的正整数.试求所有满足上述条件的集合
为给定的正整数.试求所有满足上述条件的集合![]() .
.
【答案】见解析
【解析】
记![]() .若存在有限子集
.若存在有限子集![]() ,满足
,满足![]() .
.
首先证明:存在映射![]() ,对任意的集合
,对任意的集合![]() ,均有
,均有![]() .
.
设集合![]() 的全部子集构成的集合为
的全部子集构成的集合为![]() ,
,
其中,![]() ,
,![]() ,
,![]() ,
,![]() .
.
定义映射![]() ,
,![]() ,
,![]() ,则对任意的
,则对任意的![]() ,均有
,均有![]() .
.
定义映射![]() ,对于任意的
,对于任意的![]() ,设
,设![]() ,
,![]() .则
.则![]() .
.
定义
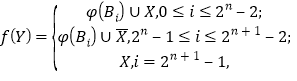
其中,![]() .则对任意的
.则对任意的![]() ,均有
,均有![]() .
.
因此,对于映射![]() ,若不存在集合
,若不存在集合![]() ,使得
,使得![]() ,则
,则![]() .
.
其次证明:对任何有限集![]() ,
,![]() ,均满足题设条件.
,均满足题设条件.
反证法.
假设存在映射![]() ,使得对任意的
,使得对任意的![]() ,均有
,均有![]() .
.
任取![]() ,由
,由![]() 是有限集,故必存在整数
是有限集,故必存在整数![]() ,使得
,使得![]() ,且对任意的
,且对任意的![]() 、
、![]() ,有
,有![]() .
.
设![]() .则
.则![]() .
.
同理,![]() ,
,![]() ,……
,……
![]() .
.
由此知![]() .
.
所以,![]() ,与
,与![]() 不含不为1的奇数因子矛盾.
不含不为1的奇数因子矛盾.
因此,不存在这样的映射![]() ,使得对任意的
,使得对任意的![]() ,均有
,均有![]() ,即对任一映射
,即对任一映射![]() ,均存在
,均存在![]() ,有
,有![]() .
.
从而,![]() 必为所有元素个数小于或等于
必为所有元素个数小于或等于![]() 的实数的集合.
的实数的集合.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:高中数学 来源: 题型:
【题目】经调查,3个成年人中就有一个高血压,那么什么是高血压?血压多少是正常的?经国际卫生组织对大量不同年龄的人群进行血压调查,得出随年龄变化,收缩压的正常值变化情况如下表:

其中: 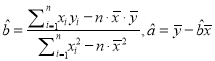 ,
, ![]() ,
, ![]()
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;(
;(![]() 的值精确到0.01)
的值精确到0.01)
(3)若规定,一个人的收缩压为标准值的0.9~1.06倍,则为血压正常人群;收缩压为标准值的1.06~1.12倍,则为轻度高血压人群;收缩压为标准值的1.12~1.20倍,则为中度高血压人群;收缩压为标准值的1.20倍及以上,则为高度高血压人群.一位收缩压为180mmHg的70岁的老人,属于哪类人群?
【答案】(1)答案见解析;(2) ![]() ;(3)中度高血压人群.
;(3)中度高血压人群.
【解析】试题分析:(1)将数据对应描点,即得散点图,(2)先求均值,再代人公式求![]() ,利用
,利用![]() 求
求![]() ,(3)根据回归直线方程求自变量为180时对应函数值,再求与标准值的倍数,确定所属人群.
,(3)根据回归直线方程求自变量为180时对应函数值,再求与标准值的倍数,确定所属人群.
试题解析:(1) 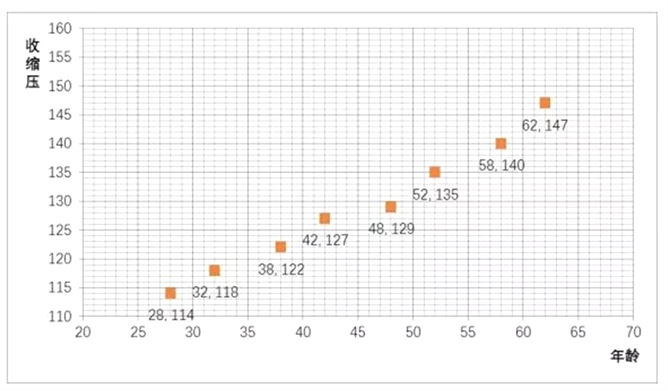
(2)![]()
![]()
∴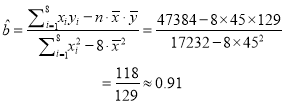
![]()
∴回归直线方程为![]() .
.
(3)根据回归直线方程的预测,年龄为70岁的老人标准收缩压约为![]() (mmHg)∵
(mmHg)∵![]()
∴收缩压为180mmHg的70岁老人为中度高血压人群.
【题型】解答题
【结束】
19
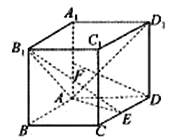
【题目】如图,四棱柱![]() 的底面为菱形,
的底面为菱形, ![]() ,
, ![]() ,
, ![]() 为
为![]() 中点.
中点.
(1)求证: ![]() 平面
平面![]() ;
;
(2)若![]() 底面
底面![]() ,且直线
,且直线![]() 与平面
与平面![]() 所成线面角的正弦值为
所成线面角的正弦值为![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设等比数列![]() 的公比为
的公比为![]() ,其前
,其前![]() 项和为
项和为![]() ,前
,前![]() 项之积为
项之积为![]() ,并且满足条件:
,并且满足条件:![]() ,
,![]() ,
,![]() ,下列结论中正确的是( )
,下列结论中正确的是( )
A. ![]() B.
B. ![]()
C. ![]() 是数列
是数列![]() 中的最大值 D. 数列
中的最大值 D. 数列![]() 无最小值
无最小值
查看答案和解析>>
科目:高中数学 来源: 题型:
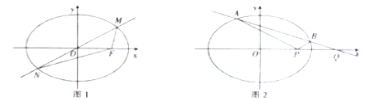
【题目】如图,已知椭圆![]() 的右焦点为
的右焦点为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,过原点
上,过原点![]() 的直线与椭圆
的直线与椭圆![]() 相交于
相交于![]() 、
、![]() 两点,且
两点,且![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设![]() ,
,![]() ,过点
,过点![]() 且斜率不为零的直线与椭圆
且斜率不为零的直线与椭圆![]() 相交于
相交于![]() 、
、![]() 两点,证明:
两点,证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为直平行六面体.命题
为直平行六面体.命题![]() 为正方体;命题
为正方体;命题![]() 的任意体对角线与其不相交的面对角线垂直.则命题
的任意体对角线与其不相交的面对角线垂直.则命题![]() 是命题
是命题![]() 的( )条件 .
的( )条件 .
A. 充分不必要 B. 必要不充分 C. 充分必要 D. 既不充分也不必要
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点到直线
的焦点到直线![]() 的距离为
的距离为![]() .
.
(1)求抛物线的标准方程;
(2)设点![]() 是抛物线上的动点,若以点
是抛物线上的动点,若以点![]() 为圆心的圆在
为圆心的圆在![]() 轴上截得的弦长均为4,求证:圆
轴上截得的弦长均为4,求证:圆![]() 恒过定点.
恒过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,已知菱形![]() 的对角线
的对角线![]() 交于点
交于点![]() ,点
,点![]() 为线段
为线段![]() 的中点,
的中点,![]() ,
,![]() ,将三角形
,将三角形![]() 沿线段
沿线段![]() 折起到
折起到![]() 的位置,
的位置,![]() ,如图2所示.
,如图2所示.

(Ⅰ)证明:平面![]()
![]() 平面
平面![]() ;
;
(Ⅱ)求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C的参数方程为![]() ,(θ为参数),以原点为极点,x轴非负半轴为极轴建立极坐标系.
,(θ为参数),以原点为极点,x轴非负半轴为极轴建立极坐标系.
(1)求曲线C的极坐标方程;
(2)在平面直角坐标系xOy中,A(﹣2,0),B(0,﹣2),M是曲线C上任意一点,求△ABM面积的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com