
分析 通分化简代入即可得出.
解答 解:$({\frac{a^2}{{{a^2}+2ab+{b^2}}}-\frac{a}{a+b}})÷({\frac{a^2}{{{a^2}-{b^2}}}-\frac{b}{a-b}-1})$=$\frac{{a}^{2}-a(a+b)}{(a+b)^{2}}$×$\frac{{a}^{2}-{b}^{2}}{{a}^{2}-b(a+b)-({a}^{2}-{b}^{2})}$
=$\frac{-ab}{a+b}$×$\frac{a-b}{-ab}$
=$\frac{a-b}{a+b}$,
又a=$\sqrt{3}$+2,b=$\sqrt{3}$-2.
∴原式=$\frac{(\sqrt{3}+2)-(\sqrt{3}-2)}{(\sqrt{3}+2)+(\sqrt{3}-2)}$
=$\frac{4}{2\sqrt{3}}$
=$\frac{2\sqrt{3}}{3}$.
点评 本题考查了代数式的化简求值、乘法公式,考查了推理能力与计算能力,属于中档题.


 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
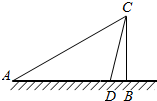 如图,某人欲测量某建筑物的高度BC,在A处测得建筑物顶端C的仰角为30°,然后,向建筑物方向前进200m到达D处,在D处测得C的仰角为75°,则建筑物的高度为( )
如图,某人欲测量某建筑物的高度BC,在A处测得建筑物顶端C的仰角为30°,然后,向建筑物方向前进200m到达D处,在D处测得C的仰角为75°,则建筑物的高度为( )| A. | 50($\sqrt{3}$+1)m | B. | 50($\sqrt{2}$+1)m | C. | 50($\sqrt{3}$-1)m | D. | 50($\sqrt{3}$+$\sqrt{2}$) m |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ②③④ | B. | ②③ | C. | ②④ | D. | ①②③ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 9 | B. | 12 | C. | 15 | D. | 16 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com