解:(I)∵c=2,C=60°,
由余弦定理c
2=a
2+b
2-2abcosC得:a
2+b
2-ab=4,
根据三角形的面积S=
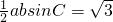
,可得ab=4,
联立方程组

,
解得a=2,b=2;
(II)由题意
sin(B+A)+sin(B-A)=4sinAcosA,
即sinBcosA=2sinAcosA,

;
当cosA≠0时,得sinB=2sinA,
由正弦定理得b=2a,
联立方程组
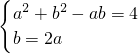
解得a=
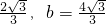
.
所以△ABC的面积S=
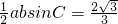
.
分析:(I)由C的度数求出sinC和cosC的值,利用余弦定理表示出c
2,把c和cosC的值代入得到一个关于a与b的关系式,再由sinC的值及三角形的面积等于

,利用面积公式列出a与b的另一个关系式,两个关系式联立即可即可求出a与b的值;
(II)由三角形的内角和定理得到C=π-(A+B),进而利用诱导公式得到sinC=sin(A+B),代入已知的等式中,左边利用和差化积公式变形,右边利用二倍角的正弦函数公式变形,分两种情况考虑:若cosA为0,得到A和B的度数,进而根据直角三角形的性质求出a与b的值;若cosA不为0,等式两边除以cosA,得到sinB=2sinA,再利用正弦定理化简得到b=2a,与第一问中余弦定理得到的a与b的关系式联立,求出a与b的值,综上,由求出的a与b的值得到ab的值,再由sinC的值,利用三角形的面积公式即可求出三角形ABC的面积.
点评:此题考查了正弦定理,余弦定理,和差化积公式,二倍角的正弦函数公式,三角形的面积公式,以及特殊角的三角函数值,其中正弦定理及余弦定理很好的解决了三角形的边角关系,熟练掌握定理及公式是解本题的关键.


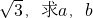 ;
;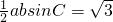 ,可得ab=4,
,可得ab=4, ,
, ;
;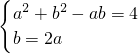
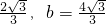 .
.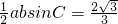 .
. ,利用面积公式列出a与b的另一个关系式,两个关系式联立即可即可求出a与b的值;
,利用面积公式列出a与b的另一个关系式,两个关系式联立即可即可求出a与b的值;

 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案