
【题目】如图所示,三棱锥![]() 中,面
中,面![]() 面
面![]() .
.
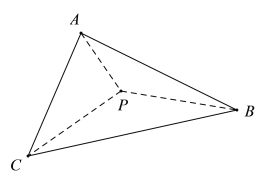
(1)若![]() ,求证:
,求证:![]() 面
面![]() ;
;
(2)若![]() ,
,![]() ,
,![]() ,且
,且![]() 和
和![]() 互余,求直线
互余,求直线![]() 和面
和面![]() 所成角的正弦值.
所成角的正弦值.
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:高中数学 来源: 题型:
【题目】如图是某学校高三年级的三个班在一学期内的六次数学测试的平均成绩y关于测试序号x的函数图象,为了容易看出一个班级的成绩变化,将离散的点用虚线连接,根据图象,给出下列结论:

①一班成绩始终高于年级平均水平,整体成绩比较好;
②二班成绩不够稳定,波动程度较大;
③三班成绩虽然多次低于年级平均水平,但在稳步提升.
其中错误的结论的个数为( )
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:过椭圆上的一点(不与长轴的端点重合)与椭圆的两个焦点确定的三角形称为椭圆的焦点三角形;已知过椭圆![]() 上一点P(不与长轴的端点重合)的焦点三角形
上一点P(不与长轴的端点重合)的焦点三角形![]() ,且
,且![]() .
.
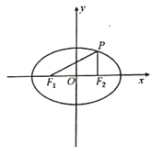
(1)求证:焦点三角形![]() 的面积为定值
的面积为定值![]() ;
;
(2)已知椭圆![]() 的一个焦点三角形为
的一个焦点三角形为![]() ,
,![]() ;
;
①若![]() ,求
,求![]() 点的横坐标的范围;
点的横坐标的范围;
②若![]() ,过点
,过点![]() 的直线
的直线![]() 与
与![]() 轴交于点
轴交于点![]() ,且
,且![]() ,记
,记![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,上顶点为
,上顶点为![]() ,则
,则![]() 的坐标为_____________,直线
的坐标为_____________,直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() 的重心恰为点
的重心恰为点![]() ,则直线
,则直线![]() 斜率为_____________.
斜率为_____________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知参加某项活动的六名成员排成一排合影留念,且甲乙两人均在丙领导人的同侧,则不同的排法共有( )
A. 240种 B. 360种 C. 480种 D. 600种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() ,F1,F2是双曲线的左右两个焦点,P在双曲线上且在第一象限,圆M是△F1PF2的内切圆.则M的横坐标为_________,若F1到圆M上点的最大距离为
,F1,F2是双曲线的左右两个焦点,P在双曲线上且在第一象限,圆M是△F1PF2的内切圆.则M的横坐标为_________,若F1到圆M上点的最大距离为![]() ,则△F1PF2的面积为___________.
,则△F1PF2的面积为___________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小区楼顶成一种“楔体”形状,该“楔体”两端成对称结构,其内部为钢架结构(未画出全部钢架,如图1所示,俯视图如图2所示),底面![]() 是矩形,
是矩形,![]() 米,
米,![]() 米,屋脊
米,屋脊![]() 到底面
到底面![]() 的距离即楔体的高为1.5米,钢架所在的平面
的距离即楔体的高为1.5米,钢架所在的平面![]() 与
与![]() 垂直且与底面的交线为
垂直且与底面的交线为![]() ,
,![]() 米,
米,![]() 为立柱且O是
为立柱且O是![]() 的中点.
的中点.
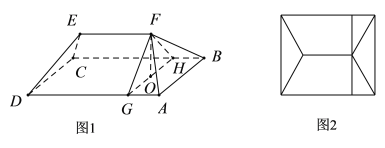
(1)求斜梁![]() 与底面
与底面![]() 所成角的大小(结果用反三角函数值表示);
所成角的大小(结果用反三角函数值表示);
(2)求此模体![]() 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com