
【题目】根据国家环保部新修订的《 环境空气质量标准》规定:居民区![]() 的年平均浓度不得超过
的年平均浓度不得超过![]() 微克/立方米,
微克/立方米,![]() 的
的![]() 小时平均浓度不得超过
小时平均浓度不得超过![]() 微克/立方米.我市环保局随机抽取了一居民区
微克/立方米.我市环保局随机抽取了一居民区![]() 年
年![]() 天
天![]() 的
的![]() 小时平均浓度(单位:微克/立方米)的监测数据,数据统计如下表:
小时平均浓度(单位:微克/立方米)的监测数据,数据统计如下表:
组别 |
| 频数(天) | 频率 |
第一组 |
|
|
|
第二组 |
|
|
|
第三组 |
|
|
|
第四组 |
|
|
|
(1)这![]() 天的测量结果按上表中分组方法绘制成的样本频率分布直方图如图.
天的测量结果按上表中分组方法绘制成的样本频率分布直方图如图.

①求图中![]() 的值;
的值;
②求样本平均数,并根据样本估计总体的思想,从![]() 的年平均浓度考虑,判断该居民区的环境质量是否需要改善?并说明理由;
的年平均浓度考虑,判断该居民区的环境质量是否需要改善?并说明理由;
(2)将频率视为概率,对于![]() 年的某
年的某![]() 天,记这
天,记这![]() 天中该居民区
天中该居民区![]() 的
的![]() 小时平均浓度符合环境空气质量标准的天数为
小时平均浓度符合环境空气质量标准的天数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
【答案】(1)①![]() ;②需要改进,理由见解析;(2)分布列见解析,
;②需要改进,理由见解析;(2)分布列见解析,![]() .
.
【解析】
(1)①根据频率分布直方图中所有矩形的面积之和为![]() 可求得
可求得![]() 的值;
的值;
②根据频率直方图计算出![]() 年该居民区
年该居民区![]() 年平均浓度,与
年平均浓度,与![]() 作大小比较,由此可得出结论;
作大小比较,由此可得出结论;
(2)由题意可知![]() ,进而可得出随机变量
,进而可得出随机变量![]() 的分布列,由此可计算得出随机变量
的分布列,由此可计算得出随机变量![]() 的数学期望值.
的数学期望值.
(1)①在频率分布直方图中,所有矩形面积之和为![]() ,
,
则![]() ,解得
,解得![]() ;
;
②![]() 年该居民区
年该居民区![]() 年平均浓度为
年平均浓度为![]() (微克/立方米),
(微克/立方米),
因为![]() ,所以
,所以![]() 年该居民区
年该居民区![]() 年平均浓度不符合环境空气质量标准,故该居民区的环境需要改进;
年平均浓度不符合环境空气质量标准,故该居民区的环境需要改进;
(2)由题意,![]() 的
的![]() 小时平均浓度符合环境空气质量标准的概率为
小时平均浓度符合环境空气质量标准的概率为![]() ,
,
![]() 的可能取值为
的可能取值为![]() 、
、![]() 、
、![]() 、
、![]() ,且
,且![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() .
.
所以,随机变量![]() 的分布列如下表所示:
的分布列如下表所示:
|
|
|
|
|
|
|
|
|
|
所以,随机变量![]() 的数学期望为
的数学期望为![]() .
.


 步步高达标卷系列答案
步步高达标卷系列答案科目:高中数学 来源: 题型:
【题目】CPI是居民消费价格指数的简称,是一个反映居民家庭一般所购买的消费品和服务项目价格水平变动情况的宏观经济指标.同比一般情况下是今年第n月与去年第n月比;环比,表示连续2个统计周期(比如连续两月)内的量的变化比.如图是根据国家统计局发布的2019年4月—2020年4月我国CPI涨跌幅数据绘制的折线图,根据该折线图,则下列说法正确的是( )
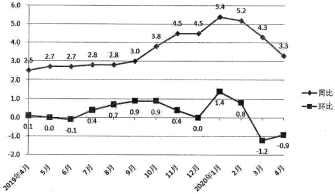
A.2020年1月CPI同比涨幅最大
B.2019年4月与同年12月相比较,4月CPI环比更大
C.2019年7月至12月,CPI一直增长
D.2020年1月至4月CPI只跌不涨
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】美团外卖和百度外卖两家公司其“骑手”的日工资方案如下:美团外卖规定底薪70元,每单抽成1元;百度外卖规定底薪100元,每日前45单无抽成,超出45单的部分每单抽成6元,假设同一公司的“骑手”一日送餐单数相同,现从两家公司个随机抽取一名“骑手”并记录其100天的送餐单数,得到如下条形图:
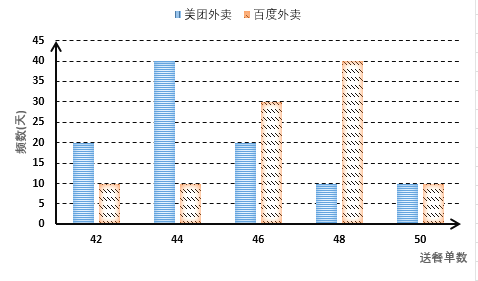
(Ⅰ)求百度外卖公司的“骑手”一日工资![]() (单位:元)与送餐单数
(单位:元)与送餐单数![]() 的函数关系;
的函数关系;
(Ⅱ)若将频率视为概率,回答下列问题:
①记百度外卖的“骑手”日工资为![]() (单位:元),求
(单位:元),求![]() 的分布列和数学期望;
的分布列和数学期望;
②小明拟到这两家公司中的一家应聘“骑手”的工作,如果仅从日收入的角度考虑,请你利用所学的统计学知识为他作出选择,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知离心率为![]() 的椭圆
的椭圆![]() 的左顶点为
的左顶点为![]() ,左焦点为
,左焦点为![]() ,及点
,及点![]() ,且
,且![]() 、
、![]() 、
、![]() 成等比数列.
成等比数列.
(1)求椭圆![]() 的方程;
的方程;
(2)斜率不为![]() 的动直线
的动直线![]() 过点
过点![]() 且与椭圆
且与椭圆![]() 相交于
相交于![]() 、
、![]() 两点,记
两点,记![]() ,线段
,线段![]() 上的点
上的点![]() 满足
满足![]() ,试求
,试求![]() (
(![]() 为坐标原点)面积的取值范围.
为坐标原点)面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小赵和小王约定在早上![]() 至
至![]() 之间到某公交站搭乘公交车去上学,已知在这段时间内,共有
之间到某公交站搭乘公交车去上学,已知在这段时间内,共有![]() 班公交车到达该站,到站的时间分别为
班公交车到达该站,到站的时间分别为![]() ,
,![]() ,如果他们约定见车就搭乘,则小赵和小王恰好能搭乘同一班公交车去上学的概率为__________.
,如果他们约定见车就搭乘,则小赵和小王恰好能搭乘同一班公交车去上学的概率为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在新型冠状病毒疫情期间,商业活动受到很大影响某小型零售连锁店总部统计了本地区50家加盟店2月份的零售情况,统计数据如图所示.据估计,平均销售收入比去年同期下降40%,则去年2月份这50家加盟店的平均销售收入约为( )
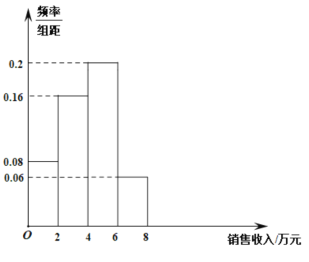
A.6.6万元B.3.96万元C.9.9万元D.7.92万元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假设你有一笔资金,现有三种投资方案,这三种方案的回报如下:
方案一:每天回报40元;
方案二:第一天回报10元,以后每天比前一天多回报10元;
方案三:第一天回报0.4元,以后每天的回报比前一天翻一番.
现打算投资10天,三种投资方案的总收益分别为![]() ,
,![]() ,
,![]() ,则( )
,则( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com