练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知直线的极坐标方程是,以极点为平面直角坐标系的原点,极轴为轴的正半轴，建立平面直角坐标系,曲线C的参数方程是,（为参数）.

    （1）求直线被曲线C截得的弦长；

    （2）从极点作曲线C的弦,求各弦中点轨迹的极坐标方程.

    【答案】（1）；（2）.

    【解析】

    （1）求得直线和曲线的直角坐标方程，利用弦长求得弦长.（2）根据曲线的参数方程，求得中点的参数方程，消去参数后求得中点轨迹的直角坐标方程，并转化为极坐标方程.

    （1）由题意可知,直线l的直角坐标系方程是,

    曲线C的普通方程是,

    则圆心C到直线l的距离,

    故所求的弦长是

    （2）从极点作曲线C的弦,弦的中点的轨迹的参数方程为,（为参数）,

    且,其普通方程为,

    极坐标方程为,化简得.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数是定义在上的奇函数，当时，．

    （1）求在上的解析式；

    （2）若，函数，是否存在实数使得的最小值为，若存在，求的值；若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数．

    （1）求函数的单调区间；

    （2）若函数的图象在点处的切线的斜率为1，问：在什么范围取值时，对于任意的，函数在区间上总存在极值？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，已知椭圆C：的左、右项点分别为A1，A2，左右焦点分别为F1，F2，离心率为，|F1F2|=，O为坐标原点．

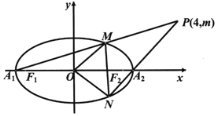
    （1）求椭圆C的方程；

    （2）设过点P（4，m）的直线PA1，PA2与椭圆分别交于点M，N，其中m＞0，求的面积S的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】年月日，小刘从各个渠道融资万元，在某大学投资一个咖啡店，年月日正式开业，已知开业第一年运营成本为万元，由于工人工资不断增加及设备维修等，以后每年成本增加万元，若每年的销售额为万元，用数列表示前年的纯收入．（注：纯收入前年的总收入前年的总支出投资额）

    （1）试求年平均利润最大时的年份（年份取正整数）并求出最大值．

    （2）若前年的收入达到最大值时，小刘计划用前年总收入的对咖啡店进行重新装修，请问：小刘最早从哪一年对咖啡店进行重新装修（年份取整数）？并求小刘计划装修的费用．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，曲线y＝f(x)在点(1，f(1))处的切线方程为y＝x.

    （1）求函数f(x)的单调区间及极值；

    （2）若x≥1，f(x)≤kx恒成立，求k的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，．

    （1）若不等式对任意的恒成立，求实数的取值范围；

    （2）记表示中的最小值，若函数在内恰有一个零点，求实的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】由0，1，2，3，4，5，6，7，8，9组成没有重复数字的五位数，且是奇数，其中恰有两个数字是偶数，则这样的五位数的个数为（ ）．

    A.7200B.6480C.4320D.5040

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知抛物线，是坐标原点，点是抛物线上一点（与坐标原点不重合），圆是以线段为直径的圆。

    （1）若点坐标为，求抛物线方程以及圆方程；

    （2）若，以线段为直径的圆与抛物线交于点（与点不重合），求圆面积的最小值。

    查看答案和解析>>

    同步练习册答案