

思路解析:解决最值问题应先构造以圆柱的半径为自变量、以它的侧面积为函数的函数表达式、然后分析函数的类型、再求侧面积的最大值.这是两个旋转体的组合、研究时、应取圆柱的轴截面图形、将它转化为平面几何的问题来解决.
解:如题图、取圆柱的轴截面ABCD、则⊙O为球的一个大圆.
设圆柱的底面半径为r、高为h、侧面积为S、
连结OB,作OH⊥AB、交AB于H.
在Rt△OBH中,有(![]() )2=R2-r2,即h=
)2=R2-r2,即h=![]()
∴S=2πrh=2πr·![]()
∴S2=16π2r2(![]() )2=-16π2r2(r2)2+16π2R2r2.
)2=-16π2r2(r2)2+16π2R2r2.
∵这是一个关于r2的二次函数、
∴当r2=-![]() 时,S有最大值、最大值为4π·
时,S有最大值、最大值为4π·![]() =2πR2.
=2πR2.
故当这圆柱的底面半径为![]() R时,它的侧面积最大,最大值是2πR2.
R时,它的侧面积最大,最大值是2πR2.
另:求S2=16π2r2(R2-r2)的最大值时还可考虑运用重要不等式S2≤16π2(![]() )2=4π2R4.∴S≤2πR2.当且仅当r2=R2-r2,即r2=
)2=4π2R4.∴S≤2πR2.当且仅当r2=R2-r2,即r2=![]() ,r=
,r=![]() R时等号成立.故S的最大值为2πR2.
R时等号成立.故S的最大值为2πR2.


科目:高中数学 来源: 题型:
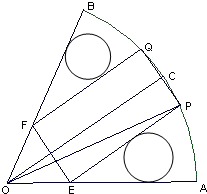 如图,在半径为R、圆心角为
如图,在半径为R、圆心角为| π | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在半径为R、圆心角为
如图,在半径为R、圆心角为 的扇形金属材料中剪出一个长方形EPQF,并且EP与∠AOB的平分线OC平行,设∠POC=θ.
的扇形金属材料中剪出一个长方形EPQF,并且EP与∠AOB的平分线OC平行,设∠POC=θ.查看答案和解析>>
科目:高中数学 来源:2012-2013学年江苏省连云港市东海高级中学高三(上)段考数学试卷(理科)(解析版) 题型:解答题
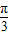 的扇形金属材料中剪出一个长方形EPQF,并且EP与∠AOB的平分线OC平行,设∠POC=θ.
的扇形金属材料中剪出一个长方形EPQF,并且EP与∠AOB的平分线OC平行,设∠POC=θ.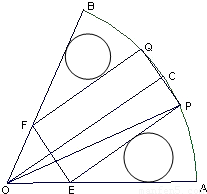
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com