
分析 作图,从而可得$\overrightarrow{OF}$=-4$\overrightarrow{OD}$,从而解得.
解答 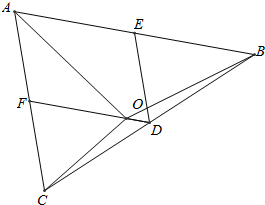 解:作图如右图,
解:作图如右图,
∵$\overrightarrow{OA}$+4$\overrightarrow{OB}$+5$\overrightarrow{OC}$=$\overrightarrow{0}$,
∴$\overrightarrow{OA}$+$\overrightarrow{OC}$=-4($\overrightarrow{OB}$+$\overrightarrow{OC}$),
∵$\overrightarrow{OA}$+$\overrightarrow{OC}$=2$\overrightarrow{OF}$,$\overrightarrow{OB}$+$\overrightarrow{OC}$=2$\overrightarrow{OD}$,
∴$\overrightarrow{OF}$=-4$\overrightarrow{OD}$,
设O到AC的距离为d,O到DE的距离为e,
则B到AC的距离为2(d+e),
∵$\overrightarrow{OF}$=-4$\overrightarrow{OD}$,
∴$\frac{d}{e}$=4,
故$\frac{d}{2(d+e)}$=$\frac{2}{5}$,
故△AOC与△ABC的面积之比是$\frac{2}{5}$.
故答案为:$\frac{2}{5}$.
点评 本题考查了平面向量的线性运算的应用及数形结合的思想应用.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{x}{y}+\frac{y}{x}$ | B. | $\frac{{{x^2}+3}}{{\sqrt{{x^2}+2}}}$ | C. | 5x+5-x | D. | tanx+cotx |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{π}{8}$+2kπ,$\frac{5π}{8}$+2kπ](k∈Z) | B. | [$\frac{π}{8}$+kπ,$\frac{5π}{8}$+kπ](k∈Z) | ||
| C. | [-$\frac{3π}{8}$+2kπ,$\frac{π}{8}$+2kπ](k∈Z) | D. | [-$\frac{3π}{8}$+kπ,$\frac{π}{8}$+kπ](k∈Z) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
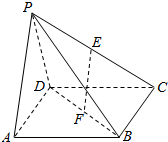 在四棱锥P-ABCD中,底面ABCD是正方形,AP⊥PD,侧面PAD⊥底面ABCD,点E、F分别为PC、BD的中点.
在四棱锥P-ABCD中,底面ABCD是正方形,AP⊥PD,侧面PAD⊥底面ABCD,点E、F分别为PC、BD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{3}$ | B. | 4$\sqrt{3}$ | C. | 8$\sqrt{3}$ | D. | 16$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 1 | C. | $\frac{17}{4}$ | D. | $\frac{15}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com