
已知 是
是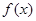 的导函数,
的导函数, ,且函数
,且函数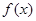 的图象过点
的图象过点 .
.
(1)求函数 的表达式;
的表达式;
(2)求函数 的单调区间和极值.
的单调区间和极值.
 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:解答题
已知函数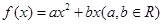 ,函数
,函数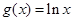 .
.
⑴当 时,函数
时,函数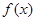 的图象与函数
的图象与函数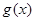 的图象有公共点,求实数
的图象有公共点,求实数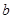 的最大值;
的最大值;
⑵当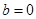 时,试判断函数
时,试判断函数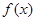 的图象与函数
的图象与函数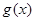 的图象的公共点的个数;
的图象的公共点的个数;
⑶函数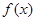 的图象能否恒在函数
的图象能否恒在函数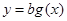 的上方?若能,求出
的上方?若能,求出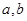 的取值范围;若不能,请说明理由.
的取值范围;若不能,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
近年来,某企业每年消耗电费约24万元,为了节能减排,决定安装一个可使用15年的太阳能供电设备接入本企业电网,安装这种供电设备的工本费(单位:万元)与太阳能电池板的面积(单位:平方米)成正比,比例系数约为0.5.为了保证正常用电,安装后采用太阳能和电能互补供电的模式.假设在此模式下,安装后该企业每年消耗的电费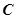 (单位:万元)与安装的这种太阳能电池板的面积
(单位:万元)与安装的这种太阳能电池板的面积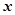 (单位:平方米)之间的函数关系是
(单位:平方米)之间的函数关系是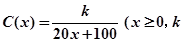 为常数).记
为常数).记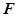 为该村安装这种太阳能供电设备的费用与该村15年共将消耗的电费之和.
为该村安装这种太阳能供电设备的费用与该村15年共将消耗的电费之和.
(1)试解释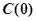 的实际意义,并建立
的实际意义,并建立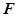 关于
关于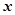 的函数关系式;
的函数关系式;
(2)当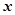 为多少平方米时,
为多少平方米时,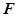 取得最小值?最小值是多少万元?
取得最小值?最小值是多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
用白铁皮做一个平底、圆锥形盖的圆柱形粮囤,粮囤容积为 (不含锥形盖内空间),盖子的母线与底面圆半径的夹角为
(不含锥形盖内空间),盖子的母线与底面圆半径的夹角为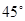 ,设粮囤的底面圆半径为R
,设粮囤的底面圆半径为R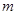 ,需用白铁皮的面积记为
,需用白铁皮的面积记为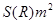 (不计接头等)。
(不计接头等)。
(1)将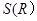 表示为R的函数;
表示为R的函数;
(2)求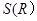 的最小值及对应的粮囤的总高度。(含圆锥顶盖)
的最小值及对应的粮囤的总高度。(含圆锥顶盖)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com