
【题目】交通指数是交通拥堵指数的简称,是综合反映道路网畅通或拥堵的概念.记交通指数为![]() ,其范围为
,其范围为![]() ,分别有5个级别:
,分别有5个级别:![]() 畅通;
畅通;![]() 基本畅通;
基本畅通;![]() 轻度拥堵;
轻度拥堵;![]() 中度拥堵;
中度拥堵;![]() 严重拥堵.早高峰时段(
严重拥堵.早高峰时段(![]() ),从贵阳市交通指挥中心随机选取了二环以内50个交通路段,依据交通指数数据绘制的直方图如图所示:
),从贵阳市交通指挥中心随机选取了二环以内50个交通路段,依据交通指数数据绘制的直方图如图所示:

(1)据此直方图估算交通指数![]() 时的中位数和平均数;
时的中位数和平均数;
(2)据此直方图求出早高峰二环以内的3个路段至少有两个严重拥堵的概率是多少?
(3)某人上班路上所用时间若畅通时为20分钟,基本畅通为30分钟,轻度拥堵为35分钟,中度拥堵为45分钟,严重拥堵为60分钟,求此人所用时间的数学期望.
科目:高中数学 来源: 题型:
【题目】甲乙两个班级均为40人,进行一门考试后,按学生考试成绩及 格与不及格进行统计,甲班及格人数为36人,乙班及格人数为24人.
(1) 根据以上数据建立一个![]() 的列联表;
的列联表;
(2) 试判断成绩与班级是否有关?
参考公式:![]() ,其中
,其中![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了得到函数y=sin(2x+ ![]() )的图象,只需将y=sin2x的图象上每一个点( )
)的图象,只需将y=sin2x的图象上每一个点( )
A.横坐标向左平移 ![]() 个单位
个单位
B.横坐标向右平移 ![]() 个单位
个单位
C.横坐标向左平移 ![]() 个单位
个单位
D.横坐标向右平移 ![]() 个单位
个单位
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】自选题:已知曲线C1: ![]() (θ为参数),曲线C2:
(θ为参数),曲线C2: 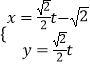 (t为参数).
(t为参数).
(1)指出C1 , C2各是什么曲线,并说明C1与C2公共点的个数;
(2)若把C1 , C2上各点的纵坐标都压缩为原来的一半,分别得到曲线C1′,C2′.写出C1′,C2′的参数方程.C1′与C2′公共点的个数和C与C2公共点的个数是否相同?说明你的理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|x≤﹣1或x≥5},集合B={x|2a≤x≤a+2}.
(1)若a=﹣1,求A∩B和A∪B;
(2)若A∩B=B,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() ,
, ![]() 是坐标原点,
是坐标原点, ![]() 分别为其左右焦点,
分别为其左右焦点, ![]() ,
, ![]() 是椭圆上一点,
是椭圆上一点, ![]() 的最大值为
的最大值为![]()
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,且
两点,且![]()
(i)求证: ![]() 为定值;
为定值;
(ii)求![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
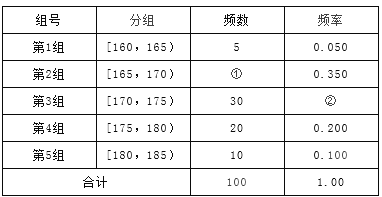
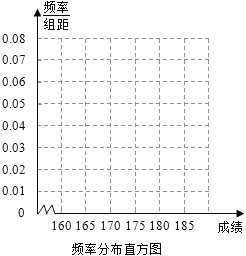
【题目】某高校在2012年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如下图所示.
(I)请先求出频率分布表中①、②位置相应数据,再在答题纸上完成下列频率分布直方图;
(Ⅱ)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试?
(Ⅲ)在(2)的前提下,学校决定在6名学生中随机抽取2名学生接受A考官的面试,求:第4组至少有一名学生被考官A面试的概率?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种产品的质量以其质量指标值衡量,并依据质量指标值划分等级如下表:
质量指标值 |
|
|
|
等级 | 三等品 | 二等品 | 一等品 |
从某企业生产的这种产品中抽取200件,检测后得到如下的频率分布直方图:
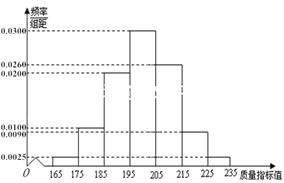
(Ⅰ)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“一、二等品至少要占全部产品92%”的规定?
(Ⅱ)在样本中,按产品等级用分层抽样的方法抽取8件,再从这8件产品中随机抽取4件,求抽取的4件产品中,一、二、三等品都有的概率;
(Ⅲ)该企业为提高产品质量,开展了“质量提升月”活动,活动后再抽样检测,产品质量指标值![]() 近似满足
近似满足![]() ,则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少?
,则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com