
【题目】底面是正方形的四棱锥中![]() 中,侧面
中,侧面![]() 底面
底面![]() ,且
,且![]() 是等腰直角三角形,其中
是等腰直角三角形,其中![]() ,
,![]() 分别为线段
分别为线段![]() 的中点,问在线段
的中点,问在线段![]() 上是否存在点
上是否存在点![]() ,使得二面角
,使得二面角![]() 的余弦值为
的余弦值为![]() ,若存在,请求出点
,若存在,请求出点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.

【答案】存在,![]() 为
为![]() 的中点.
的中点.
【解析】
试题分析:取![]() 的中点
的中点![]() ,连接
,连接![]() ,可证得
,可证得![]() 平面
平面![]() ,以
,以![]() 为原点,分别以射线
为原点,分别以射线![]() 和
和![]() 为
为![]() 轴,
轴,![]() 轴和
轴和![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() ,不妨设
,不妨设![]() ,
,![]()
![]() ,分别求出平面
,分别求出平面![]() 和平面
和平面![]() 的法向量,根据二面角的求法得到
的法向量,根据二面角的求法得到![]() 的方程,求出其值,若满足
的方程,求出其值,若满足![]() ,则存在,否则不存在.
,则存在,否则不存在.
试题解析:取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,
因为![]() ,所以
,所以![]() ,
,
又因为侧面![]() 底面
底面![]() ,交线为
,交线为![]() ,所以
,所以![]() 平面
平面![]() ,·······2分
,·······2分
以![]() 为原点,分别以射线
为原点,分别以射线![]() 和
和![]() 为
为![]() 轴,
轴,![]() 轴和
轴和![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() 如图,不妨设
如图,不妨设![]() ,
,
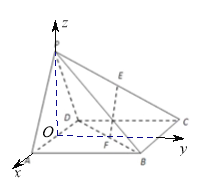
则有![]() ,假设在
,假设在![]() 上存在符合题意的点
上存在符合题意的点![]() ,
,
则![]() ,
,
因为侧面![]() 底面
底面![]() ,交线为
,交线为![]() ,且底面是正方形,
,且底面是正方形,
所以![]() 平面
平面![]() ,则
,则![]() ,
,
又![]() ,所以
,所以![]() 平面
平面![]() ,即平面
,即平面![]() 的一个法向量为
的一个法向量为![]() ,·······4分
,·······4分
设平面![]() 的法向理为
的法向理为![]() ,由
,由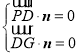 即
即![]() ,亦即
,亦即 ,可取
,可取![]() ,·······6分
,·······6分
所以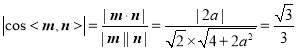 ,
,
解得![]() (舍去)
(舍去)
所以线段![]() 上存在点
上存在点![]() ,且
,且![]() 为
为![]() 的中点,使得二面角
的中点,使得二面角![]() 的余弦值为
的余弦值为![]() .·······10分
.·······10分


科目:高中数学 来源: 题型:
【题目】数列{an}满足a1=1,nan+1=(n+1)an+n(n+1),n∈N* . (Ⅰ)证明:数列{ ![]() }是等差数列;
}是等差数列;
(Ⅱ)设bn=3n ![]() ,求数列{bn}的前n项和Sn .
,求数列{bn}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,以原点O为圆心,椭圆C的长半轴长为半径的圆与直线
,以原点O为圆心,椭圆C的长半轴长为半径的圆与直线![]() 相切.
相切.
⑴求椭圆C的标准方程;
⑵已知点A、B为动直线![]() 与椭圆C的两个交点,问:在x轴上是否存在定点E,使得
与椭圆C的两个交点,问:在x轴上是否存在定点E,使得![]() 为定值?若存在,试求出点E的坐标和定值;若不存在,请说明理由.
为定值?若存在,试求出点E的坐标和定值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设常数a∈R,函数f(x)=(a﹣x)|x|.
(1)若a=1,求f(x)的单调区间;
(2)若f(x)是奇函数,且关于x的不等式mx2+m>f[f(x)]对所有的x∈[﹣2,2]恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]()
![]() 满足
满足![]() ,且
,且![]() ,正项数列
,正项数列![]() 满足
满足![]() ,其前7项和为42.
,其前7项和为42.
(1)求数列![]() 和
和![]() 的通项公式;
的通项公式;
(2)令![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,若对任意正整数
,若对任意正整数![]() ,都有
,都有![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(3)将数列![]() 的项按照“当
的项按照“当![]() 为奇数时,
为奇数时,![]() 放在前面;当
放在前面;当![]() 为偶数时,
为偶数时,![]() 放在前面”的要求进行排列,得到一个新的数列:
放在前面”的要求进行排列,得到一个新的数列:![]() ,求这个新数列的前
,求这个新数列的前![]() 项和
项和![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位有员工1000名,平均每人每年创造利润10万元.为了增加企业竞争力,决定优化产业结构,调整出x(x∈N*)名员工从事第三产业,调整后他们平均每人每年创造利润为10(a﹣ ![]() )万元(a>0),剩下的员工平均每人每年创造的利润为原来(1+
)万元(a>0),剩下的员工平均每人每年创造的利润为原来(1+ ![]() )倍.
)倍.
(1)若要保证剩余员工创造的年总利润不低于原来1000名员工创造的年总利润,则最多可以整出多少名员工从事第三产业;
(2)若调整出的员工创造的年总利润始终不高于剩余员工创造的年总利润,则a的最大取值是多少.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() 的左右顶点分别为
的左右顶点分别为![]() ,右焦点为
,右焦点为![]() ,焦距为
,焦距为![]() ,点
,点![]() 是椭圆C上异于
是椭圆C上异于![]() 两点的动点,
两点的动点, ![]() 的面积最大值为
的面积最大值为![]() .
.
(1)求椭圆C的方程;
(2)若直线![]() 与直线
与直线![]() 交于点
交于点![]() ,试判断以
,试判断以![]() 为直径的圆与直线
为直径的圆与直线![]() 的位置关系,并作出证明.
的位置关系,并作出证明.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,tanA是以﹣4为第三项,4为第七项的等差数列的公差,tanB是以2为公差,9为第五项的等差数列的第二项,则这个三角形是( )
A.锐角三角形
B.钝角三角形
C.等腰直角三角形
D.等腰或直角三角形
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一房产商竞标得一块扇形OPQ地皮,其圆心角∠POQ= ![]() ,半径为R=200m,房产商欲在此地皮上修建一栋平面图为矩形的商住楼,为使得地皮的使用率最大,准备了两种设计方案如图,方案一:矩形ABCD的一边AB在半径OP上,C在圆弧上,D在半径OQ;方案二:矩形EFGH的顶点在圆弧上,顶点G,H分别在两条半径上.请你通过计算,为房产商提供决策建议.
,半径为R=200m,房产商欲在此地皮上修建一栋平面图为矩形的商住楼,为使得地皮的使用率最大,准备了两种设计方案如图,方案一:矩形ABCD的一边AB在半径OP上,C在圆弧上,D在半径OQ;方案二:矩形EFGH的顶点在圆弧上,顶点G,H分别在两条半径上.请你通过计算,为房产商提供决策建议. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com