
ЁОЬтФПЁПвЛжжаТЕФбщбЊММЪѕПЩвдЬсИпбЊвКМьВтаЇТЪ.ЯжФГзЈвЕМьВтЛњЙЙЬсШЁСЫ![]() ЗнбЊвКбљБОЃЌЦфжажЛга1ЗнГЪбєадЃЌВЂЩшМЦСЫШчЯТЛьКЯМьВтЗНАИЃКЯШЫцЛњЖдЦфжа
ЗнбЊвКбљБОЃЌЦфжажЛга1ЗнГЪбєадЃЌВЂЩшМЦСЫШчЯТЛьКЯМьВтЗНАИЃКЯШЫцЛњЖдЦфжа![]() ЗнбЊвКбљБОЗжБ№ШЁбљЃЌШЛКѓдйЛьКЯдквЛЦ№НјааМьВтЃЌШєМьВтНсЙћЮЊвѕадЃЌдђЖдСэЭт3ЗнбЊвКж№вЛМьВтЃЌжБЕНШЗЖЈГЪбєадЕФбЊвКЮЊжЙЃЛШєМьВтНсЙћГЪбєадЃЌВтЖдет
ЗнбЊвКбљБОЗжБ№ШЁбљЃЌШЛКѓдйЛьКЯдквЛЦ№НјааМьВтЃЌШєМьВтНсЙћЮЊвѕадЃЌдђЖдСэЭт3ЗнбЊвКж№вЛМьВтЃЌжБЕНШЗЖЈГЪбєадЕФбЊвКЮЊжЙЃЛШєМьВтНсЙћГЪбєадЃЌВтЖдет![]() ЗнбЊвКдйж№вЛМьВтЃЌжБЕНШЗЖЈГЪбєадЕФбЊвКЮЊжЙ.
ЗнбЊвКдйж№вЛМьВтЃЌжБЕНШЗЖЈГЪбєадЕФбЊвКЮЊжЙ.
ЃЈ1ЃЉШє![]() ЃЌЧѓЧЁКУОЙ§3ДЮМьВтЖјШЗЖЈГЪбєадЕФбЊвКЕФЪТМўИХТЪЃЛ
ЃЌЧѓЧЁКУОЙ§3ДЮМьВтЖјШЗЖЈГЪбєадЕФбЊвКЕФЪТМўИХТЪЃЛ
ЃЈ2ЃЉШє![]() ЃЌвЫВЩгУвдЩЯЗНАИМьВтЖјШЗЖЈГЪбєадЕФбЊвКЫљашДЮЪ§ЮЊ
ЃЌвЫВЩгУвдЩЯЗНАИМьВтЖјШЗЖЈГЪбєадЕФбЊвКЫљашДЮЪ§ЮЊ![]() ЃЌ
ЃЌ
ЂйЧѓ![]() ЕФИХТЪЗжВМЃЛ
ЕФИХТЪЗжВМЃЛ
ЂкЧѓ![]() .
.
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЈ2ЃЉЂйЯъМћНтЮіЂк
ЃЈ2ЃЉЂйЯъМћНтЮіЂк![]()
ЁОНтЮіЁП
ЃЈ1ЃЉВЛТлЕквЛДЮМьВтНсЙћШчКЮЃЌЖМвЊЖдКЌга2вѕ1бєЕУбЊвКбљБОНјааж№вЛМьВтЃЌЙЪЕк2ДЮКЭЕк3ДЮМьВтЕФЖМЪЧвѕадЛђепЕк2ДЮМьВтЕФЪЧвѕадЃЌЕк3ДЮМьВтЕФЪЧбєадЃЌИљОнзщКЯЪ§ЙЋЪНКЭЙХЕфИХаЭЕФИХТЪЙЋЪНМЦЫуИХТЪЃЛ
ЃЈ2ЃЉИљОнзщКЯЪ§ЙЋЪНКЭЙХЕфИХаЭЕФИХТЪЙЋЪНвРДЮМЦЫу![]() ЃЌ3ЃЌ4ЃЌ
ЃЌ3ЃЌ4ЃЌ![]() ЃЌ
ЃЌ![]() ЕФИХТЪЃЌЕУГіЗжВМСаКЭЪ§бЇЦкЭћЃЎ
ЕФИХТЪЃЌЕУГіЗжВМСаКЭЪ§бЇЦкЭћЃЎ
НтЃКЃЈ1ЃЉдк![]() ЪБЃЌЧЁКУдкЕкШ§ДЮЪБМьВтГіГЪбєадбЊвКЃЌЫЕУїЦфжаШ§ЗнбЊвКжаЕФЦфжавЛЗнГЪбєадЃЌВЂЧвЖдКЌбєадбЊвКЕФвЛзщНјааМьВтЪБЃЌЧАСНДЮМьВтГібЊвКЮЊвѕадЃЌЛђЕквЛДЮЮЊвѕадЕкЖўДЮЮЊбєад.
ЪБЃЌЧЁКУдкЕкШ§ДЮЪБМьВтГіГЪбєадбЊвКЃЌЫЕУїЦфжаШ§ЗнбЊвКжаЕФЦфжавЛЗнГЪбєадЃЌВЂЧвЖдКЌбєадбЊвКЕФвЛзщНјааМьВтЪБЃЌЧАСНДЮМьВтГібЊвКЮЊвѕадЃЌЛђЕквЛДЮЮЊвѕадЕкЖўДЮЮЊбєад.
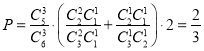
ЃЈ2ЃЉЂйдк![]() ЪБЃЌ
ЪБЃЌ![]()

![]()
ЭЌРэЃЌЕБ![]() ЪБЃЌ
ЪБЃЌ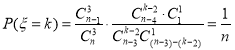
![]()
![]() ЕФЗжВМСаЮЊЃК
ЕФЗжВМСаЮЊЃК
| 2 | 3 | 4 |
|
|
|
|
|
|
|
|
|
|
Ђк![]()
![]()



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПздгЩЙКЪЧЭЈЙ§зджњНсЫуЗНЪНЙКЮяЕФвЛжжаЮЪН. ФГДѓаЭГЌЪаЮЊЕїВщЙЫПЭЪЙгУздгЩЙКЕФЧщПіЃЌЫцЛњГщШЁСЫ100ШЫЃЌЭГМЦНсЙћећРэШчЯТЃК
20вдЯТ |
|
|
|
|
| 70вдЩЯ | |
ЪЙгУШЫЪ§ | 3 | 12 | 17 | 6 | 4 | 2 | 0 |
ЮДЪЙгУШЫЪ§ | 0 | 0 | 3 | 14 | 36 | 3 | 0 |
ЃЈЂёЃЉЯжЫцЛњГщШЁ 1 УћЙЫПЭЃЌЪдЙРМЦИУЙЫПЭФъСфдк![]() ЧвЮДЪЙгУздгЩЙКЕФИХТЪЃЛ
ЧвЮДЪЙгУздгЩЙКЕФИХТЪЃЛ
ЃЈЂђЃЉДгБЛГщШЁЕФФъСфдк![]() ЪЙгУздгЩЙКЕФЙЫПЭжаЃЌЫцЛњГщШЁ3ШЫНјвЛВНСЫНтЧщПіЃЌгУ
ЪЙгУздгЩЙКЕФЙЫПЭжаЃЌЫцЛњГщШЁ3ШЫНјвЛВНСЫНтЧщПіЃЌгУ![]() БэЪОет3ШЫжаФъСфдк
БэЪОет3ШЫжаФъСфдк![]() ЕФШЫЪ§ЃЌЧѓЫцЛњБфСП
ЕФШЫЪ§ЃЌЧѓЫцЛњБфСП![]() ЕФЗжВМСаМАЪ§бЇЦкЭћЃЛ
ЕФЗжВМСаМАЪ§бЇЦкЭћЃЛ
ЃЈЂѓЃЉЮЊЙФРјЙЫПЭЪЙгУздгЩЙКЃЌИУГЌЪаФтЖдЪЙгУздгЩЙКЕФЙЫПЭдљЫЭ1ИіЛЗБЃЙКЮяДќ.ШєФГШеИУГЌЪадЄМЦга5000ШЫЙКЮяЃЌЪдЙРМЦИУГЌЪаЕБЬьжСЩйгІзМБИЖрЩйИіЛЗБЃЙКЮяДќ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЖЏЕу![]() дкЫЋЧњЯп
дкЫЋЧњЯп![]() ЩЯЃЌЫЋЧњЯп
ЩЯЃЌЫЋЧњЯп![]() ЕФзѓЁЂгвНЙЕуЗжБ№ЮЊ
ЕФзѓЁЂгвНЙЕуЗжБ№ЮЊ![]() ЁЂ
ЁЂ![]() ЃЌЯТСаНсТле§ШЗЕФЪЧЃЈ ЃЉ
ЃЌЯТСаНсТле§ШЗЕФЪЧЃЈ ЃЉ
A.![]() ЕФРыаФТЪЮЊ
ЕФРыаФТЪЮЊ![]()
B.![]() ЕФНЅНќЯпЗНГЬЮЊ
ЕФНЅНќЯпЗНГЬЮЊ![]()
C.ЖЏЕу![]() ЕНСНЬѕНЅНќЯпЕФОрРыжЎЛ§ЮЊЖЈжЕ
ЕНСНЬѕНЅНќЯпЕФОрРыжЎЛ§ЮЊЖЈжЕ
D.ЕБЖЏЕу![]() дкЫЋЧњЯп
дкЫЋЧњЯп![]() ЕФзѓжЇЩЯЪБЃЌ
ЕФзѓжЇЩЯЪБЃЌ![]() ЕФзюДѓжЕЮЊ
ЕФзюДѓжЕЮЊ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() ЃЌЦфжа
ЃЌЦфжа![]() ЃЌ
ЃЌ![]() ЮЊздШЛЖдЪ§ЕФЕзЪ§.
ЮЊздШЛЖдЪ§ЕФЕзЪ§.
ЃЈ1ЃЉШє![]() ЃЌЧѓКЏЪ§
ЃЌЧѓКЏЪ§![]() дк
дк![]() ДІЕФЧаЯпЗНГЬЃЛ
ДІЕФЧаЯпЗНГЬЃЛ
ЃЈ2ЃЉШєКЏЪ§![]() дкЖЈвхгђЩЯЧЁгаСНИіВЛЭЌЕФСуЕуЃЌЧѓЪЕЪ§aЕФШЁжЕЗЖЮЇЃЛ
дкЖЈвхгђЩЯЧЁгаСНИіВЛЭЌЕФСуЕуЃЌЧѓЪЕЪ§aЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉЩшКЏЪ§![]() дкЧјМф
дкЧјМф![]() )ЩЯДцдкМЋжЕЃЌЧѓжЄЃК
)ЩЯДцдкМЋжЕЃЌЧѓжЄЃК![]() .
.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЕБ![]() ЪБЃЌЧѓЧњЯп
ЪБЃЌЧѓЧњЯп![]() гыЧњЯп
гыЧњЯп![]() ЕФЙЋЧаЯпЕФЗНГЬЃЛ
ЕФЙЋЧаЯпЕФЗНГЬЃЛ
ЃЈ2ЃЉЩшКЏЪ§![]() ЕФСНИіМЋжЕЕуЮЊ
ЕФСНИіМЋжЕЕуЮЊ![]() ЃЌЧѓжЄЃКЙигк
ЃЌЧѓжЄЃКЙигк![]() ЕФЗНГЬ
ЕФЗНГЬ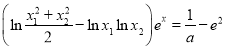 гаЮЈвЛНтЃЎ
гаЮЈвЛНтЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊFЪЧХзЮяЯпCЃКx2ЃН4yЕФНЙЕуЃЌЙ§EЃЈ0ЃЌЉ1ЃЉЕФжБЯпlгыХзЮяЯпЗжeНЛгкAЃЌBСНЕуЃЎ
ЃЈ1ЃЉЩшжБЯпAFЃЌBFЕФаБТЪЗжeЮЊk1ЃЌk2ЃЌжЄУїЃКk1+k2ЃН0ЃЛ
ЃЈ2ЃЉШє![]() ЕФУцЛ§ЮЊ
ЕФУцЛ§ЮЊ![]() ЃЌЧѓжБЯпlЕФЗНГЬЃЎ
ЃЌЧѓжБЯпlЕФЗНГЬЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП2020ФъДКНкЭЛШчЦфРДЕФаТаЭЙкзДВЁЖОЗЮбздкКўБББЌЗЂЃЌвЛЗНгаФбАЫЗНжЇдЎЃЌШЋЙњИїЕиЕФАзвТЬьЪЙзпЩЯеНГЁЕФЕквЛЯпЃЌФГвНдКГщЕїМзЁЂввСНУћвНЩњЃЌГщЕї![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() Ш§УћЛЄЪПжЇдЎЮфККЕквЛвНдКгыЕкЖўвНдКЃЌВЮМгЮфККвпЧщОбЛїеНЦфжабЁвЛУћЛЄЪПгывЛУћвНЩњШЅЕквЛвНдКЃЌЦфЫќЖМдкЕкЖўвНдКЙЄзїЃЌдђвНЩњМзКЭЛЄЪП
Ш§УћЛЄЪПжЇдЎЮфККЕквЛвНдКгыЕкЖўвНдКЃЌВЮМгЮфККвпЧщОбЛїеНЦфжабЁвЛУћЛЄЪПгывЛУћвНЩњШЅЕквЛвНдКЃЌЦфЫќЖМдкЕкЖўвНдКЙЄзїЃЌдђвНЩњМзКЭЛЄЪП![]() БЛбЁдкЕквЛвНдКЙЄзїЕФИХТЪЮЊЃЈ ЃЉ
БЛбЁдкЕквЛвНдКЙЄзїЕФИХТЪЮЊЃЈ ЃЉ
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкжБНЧзјБъЯЕ![]() жаЃЌЧњЯп
жаЃЌЧњЯп![]() ЕФВЮЪ§ЗНГЬЮЊ
ЕФВЮЪ§ЗНГЬЮЊ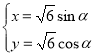 ЃЈ
ЃЈ![]() ЮЊВЮЪ§ЃЉЃЌвдзјБъдЕу
ЮЊВЮЪ§ЃЉЃЌвдзјБъдЕу![]() ЮЊМЋЕуЃЌвд
ЮЊМЋЕуЃЌвд![]() жсе§АыжсЮЊМЋжсЃЌНЈСЂМЋзјБъЯЕЃЌжБЯп
жсе§АыжсЮЊМЋжсЃЌНЈСЂМЋзјБъЯЕЃЌжБЯп![]() ЕФМЋзјБъЗНГЬЮЊ
ЕФМЋзјБъЗНГЬЮЊ![]() .
.
ЃЈ1ЃЉЧѓ![]() ЕФЦеЭЈЗНГЬКЭ
ЕФЦеЭЈЗНГЬКЭ![]() ЕФжБНЧзјБъЗНГЬЃЛ
ЕФжБНЧзјБъЗНГЬЃЛ
ЃЈ2ЃЉжБЯп![]() гы
гы![]() жсЕФНЛЕуЮЊ
жсЕФНЛЕуЮЊ![]() ЃЌОЙ§Еу
ЃЌОЙ§Еу![]() ЕФжБЯп
ЕФжБЯп![]() гыЧњЯп
гыЧњЯп![]() НЛгк
НЛгк![]() СНЕуЃЌШє
СНЕуЃЌШє![]() ЃЌЧѓжБЯп
ЃЌЧѓжБЯп![]() ЕФЧуаБНЧ.
ЕФЧуаБНЧ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩш![]() ЃЌКЏЪ§
ЃЌКЏЪ§![]() ЃЎ
ЃЎ
ЃЈЂёЃЉЬжТлКЏЪ§![]() ЕФЕЅЕїЧјМфКЭМЋжЕЃЛ
ЕФЕЅЕїЧјМфКЭМЋжЕЃЛ
ЃЈЂђЃЉвбжЊ![]() ЃЈ
ЃЈ![]() ЪЧздШЛЖдЪ§ЕФЕзЪ§ЃЉКЭ
ЪЧздШЛЖдЪ§ЕФЕзЪ§ЃЉКЭ![]() ЪЧКЏЪ§
ЪЧКЏЪ§![]() ЕФСНИіВЛЭЌЕФСуЕуЃЌЧѓ
ЕФСНИіВЛЭЌЕФСуЕуЃЌЧѓ![]() ЕФжЕВЂжЄУїЃК
ЕФжЕВЂжЄУїЃК![]() ЃЎ
ЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com