
����Ŀ��ij��ҵ�μ�![]() ��Ŀ�����Ĺ���Ϊ
��Ŀ�����Ĺ���Ϊ![]() �ˣ�ƽ��ÿ��ÿ�괴������
�ˣ�ƽ��ÿ��ÿ�괴������![]() ��Ԫ.������ʵ����Ҫ����
��Ԫ.������ʵ����Ҫ����![]() ��Ŀ�е���
��Ŀ�е���![]() �˲���
�˲���![]() ��Ŀ���ۺ��������ÿ��ÿ����Դ�������
��Ŀ���ۺ��������ÿ��ÿ����Դ�������![]() ��Ԫ��
��Ԫ��![]() ����
����![]() ��Ŀ���µĹ���ÿ��ÿ�괴����ͼ��Ҫ���
��Ŀ���µĹ���ÿ��ÿ�괴����ͼ��Ҫ���![]()
��1����Ҫ��֤![]() ��Ŀ���µĹ��˴��������������ԭ��
��Ŀ���µĹ��˴��������������ԭ��![]() �����˴�������������������������˲μ�
�����˴�������������������������˲μ�![]() ��Ŀ�����ۺ��������
��Ŀ�����ۺ��������
��2���ڣ�1���������£�����![]() ��Ŀ�������������ܳ�����������
��Ŀ�������������ܳ�����������![]() ʱ������ʹ��
ʱ������ʹ��![]() ��Ŀ�����ڹ��˴������������ʼ�ղ����ڵ����Ĺ��������������������ʵ��
��Ŀ�����ڹ��˴������������ʼ�ղ����ڵ����Ĺ��������������������ʵ��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
���𰸡���1��![]() ����2��
����2��![]() .
.
��������
��1���������⣬�г�����ʽ![]() ����⼴�ɣ�
����⼴�ɣ�
��2�����![]() �ķ�Χ���ó�����ʽ
�ķ�Χ���ó�����ʽ![]()
![]() �������ɵ�
�������ɵ�![]() �����������
�����������![]() �ķ�Χ����֪�����ڶ�������Ϊ����������
�ķ�Χ����֪�����ڶ�������Ϊ����������![]() ʱ������ȡ����Сֵ��
ʱ������ȡ����Сֵ��
�����![]() �˲μ�
�˲μ�![]() ��Ŀ�����ۺ������
��Ŀ�����ۺ������
��1��������ã�![]() ��
��
��![]() ����
����![]() ������
������![]() ����������500��Ա�����µ�����ҵ��
����������500��Ա�����µ�����ҵ��
��2������֪��![]() ��
��
���µ�����ҵ��Ա���������������Ϊ![]() ��Ԫ��
��Ԫ��
����ԭ����ҵ��Ա������������Ϊ![]() ��Ԫ��
��Ԫ��
��![]()
![]() ��
��
����![]()
![]() ��
��
����![]() ��
��
��![]() �������
�������
��Ϊ![]() ��
��
����![]() ��
��
����![]() ��
��
��![]() ������
������![]() ��
��
��![]() ��ȡֵ��ΧΪ
��ȡֵ��ΧΪ![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����̳��Ŀյ���1�µ�5�µ����������·���أ��õ���ͳ���������±���
�·� | 1 | 2 | 3 | 4 | 5 |
���� | 0.6 | 0.8 | 1.2 | 1.6 | 1.8 |
��1������������1�µ�5�µ��������������Իع�ģ����ϸ��̳��յ���������![]() ���ټ������·�
���ټ������·�![]() ֮�����ع�ϵ.������С���˷���
֮�����ع�ϵ.������С���˷���![]() ����
����![]() �����Իع鷽��
�����Իع鷽��![]() ����Ԥ��6�·ݸ��̳��յ�����������
����Ԥ��6�·ݸ��̳��յ�����������
��2�������̳���Ӫ�����Կյ�������һ�ִ�������7�µ�12���й���յ���Ը�Ĺ˿ͽ����ʾ�����.����õ����յ�������Ⱥ��ʮ���Ӵ���Ӫ�������л��������е�500���˿ͽ�����һ���������飬�õ�����һ��Ƶ������
�й�����Ը��Ӧ���·� | 7 | 8 | 9 | 10 | 11 | 12 |
Ƶ�� | 60 | 80 | 120 | 130 | 80 | 30 |
�ֲ��÷ֲ�����ķ����ӹ�����Ը���·���7����12�µ���90���˿��������ȡ6�����ٴ���6���������ȡ3�˽��и��ٵ��飬������3����ǡ����2���ǹ�����Ը���·���12�µĸ���.
�ο���ʽ�����ݣ����Իع鷽��![]() ������
������ ��
��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() �ǵ������У�����
�ǵ������У�����![]() ���㣺������
���㣺������![]() ������
������![]() ��ʹ��
��ʹ��![]() �����
�����![]() ��
��![]() �ġ��ָ����С�.
�ġ��ָ����С�.
��1����![]() ��֤��������
��֤��������![]() ��
��![]() �ķָ����У�
�ķָ����У�
��2����![]() ��
��![]() ��ǰn��ͣ�
��ǰn��ͣ�![]() ���ж�����
���ж�����![]() �Ƿ�������
�Ƿ�������![]() �ķָ����У���˵�����ɣ�
�ķָ����У���˵�����ɣ�
��3����![]() ��
��![]() ��ǰn��ͣ�������
��ǰn��ͣ�������![]() ��
��![]() �ķָ����У���ʵ��
�ķָ����У���ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��Բ![]() ��
��![]() ����Ϊ
����Ϊ![]() ��������
��������![]() ������
������![]() ��б��Ϊ
��б��Ϊ![]() ��ֱ��
��ֱ��![]() ����Բ
����Բ![]() �ڵ�
�ڵ�![]() ����
����![]() ���ڵ�
���ڵ�![]() .
.
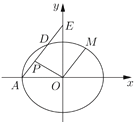
��1������Բ![]() �ķ��̣�
�ķ��̣�
��2����֪![]() Ϊ
Ϊ![]() ���е㣬
���е㣬![]() ��֤�������������
��֤�������������![]() ����
����![]() �������
�������
��3��������![]() ��ֱ��
��ֱ��![]() ��ƽ���߽���Բ
��ƽ���߽���Բ![]() �ڵ�
�ڵ�![]() ����
����![]() ����Сֵ.
����Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����Բ![]() ��
��![]() ��
��![]() ���������ǵĹ�����Ĺ켣��Ϊ����
���������ǵĹ�����Ĺ켣��Ϊ����![]() ��������
��������![]() ��
��![]() ���������Ľ���Ϊ
���������Ľ���Ϊ![]() ��������
��������![]() �ϵ���������
�ϵ���������![]() ���㣺
���㣺![]() .
.
��1��������![]() �Ĺ켣���̣�
�Ĺ켣���̣�
��2��֤��ֱ��![]() �㾭��һ���㣬����˶�������ꣻ
�㾭��һ���㣬����˶�������ꣻ
��3����![]() ���
���![]() �����ֵ.
�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��![]() ͳ��ѧ�н�
ͳ��ѧ�н�![]() ����
����![]() �ĺͼ���
�ĺͼ���![]()
��1����![]()
![]() ����
����![]() ��
��
��2���Ƿ���ڻ�����ȵķǸ�����![]() ��
��![]() ,ʹ��
,ʹ��![]() �����������ڣ���д�������Ĺ��̣�����������֤����
�����������ڣ���д�������Ĺ��̣�����������֤����
��3����![]()
![]() �Dz�ͬ����ʵ����
�Dz�ͬ����ʵ����![]() ���������
���������![]() ������
������![]() ���ж�
���ж�![]() �Ƿ�Ϊһ���ȱ����У���˵������.
�Ƿ�Ϊһ���ȱ����У���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������G�Ķ�����ԭ�㣬������y���������ϣ���P��m��4�������ߵľ������5��
��1����������G�ķ��̣�
��2����ͼ����������G�Ľ����ֱ��������������G��Բx2+��y��1��2��1����A��C��D��B�ĵ㣬��֤��|AC||BD|Ϊ��ֵ��
��3����A��B�ֱ�������G������l1��l2��l1��l2���ڵ�M�������ACM���BDM���֮�͵���Сֵ��
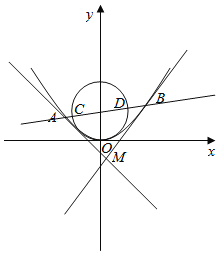
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ,
,![]() ,
,![]() ��
��![]() ���Ϻ���ְͨ
���Ϻ���ְͨ![]() (
(![]() ��
��![]() )���˵������룬����
)���˵������룬����![]() �����ݵ���λ��Ϊ
�����ݵ���λ��Ϊ![]() ��ƽ����Ϊ
��ƽ����Ϊ![]() ������Ϊ
������Ϊ![]() ������ټ�����������������
������ټ�����������������![]() ������
������![]() �������У�����˵����ȷ�� ��
�������У�����˵����ȷ�� ��
A.������ƽ�������������λ��һ���������ܲ���
B.������ƽ�������������λ�����ܲ��䣬������
C.������ƽ�������������λ�����ܲ��䣬����Ҳ����
D.������ƽ�������������λ�����ܲ��䣬������ܲ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪˫����![]() ����
����![]() ���ҽ����߷���Ϊ
���ҽ����߷���Ϊ![]() ��ֱ��
��ֱ��![]() ������
������![]() ���ڵ�
���ڵ�![]() ��
��![]() ����.
����.
��1����˫����![]() �ķ��̣�
�ķ��̣�
��2����ֱ��![]() ��ԭ�㣬��
��ԭ�㣬��![]() ������
������![]() ����һ�㣬ֱ��
����һ�㣬ֱ��![]() ��
��![]() ��б�ʶ����ڣ���Ϊ
��б�ʶ����ڣ���Ϊ![]() ��
��![]() ����̽��
����̽��![]() ��ֵ�Ƿ����
��ֵ�Ƿ����![]() ��ֱ��
��ֱ��![]() �йأ���֤����Ľ��ۣ�
�йأ���֤����Ľ��ۣ�
��3����ֱ��![]() ����
����![]() ������
������![]() �����Ƿ���ڶ���
�����Ƿ���ڶ���![]() ��ʹ��
��ʹ��![]() Ϊ�����������ڣ������
Ϊ�����������ڣ������![]() ���꼰�˳�����ֵ���������ڣ�˵������.
���꼰�˳�����ֵ���������ڣ�˵������.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com