
【题目】已知 ![]() 是两条不重合的直线,
是两条不重合的直线, ![]() 是三个两两不重合的平面,给出下列四个命题:
是三个两两不重合的平面,给出下列四个命题:
①若 ![]() ,
, ![]() ,则
,则 ![]() ;②若
;②若 ![]() ,
, ![]() ,则
,则 ![]() ;
;
③若 ![]() ,
, ![]() ,
, ![]() ,则
,则 ![]() ;④若
;④若 ![]() 是异面直线,
是异面直线, ![]() ,
, ![]() ,
, ![]() ,则
,则 ![]() .
.
其中真命题是( )
A.①和④
B.①和③
C.③和④
D.①和②
【答案】A
【解析】由线面角的定义可知答案①中的直线 ![]() ,
, ![]() ,则平面
,则平面 ![]() 是正确的;因为答案②中的两个平面
是正确的;因为答案②中的两个平面 ![]() 也可能相交,故不正确;答案③中的两个平面
也可能相交,故不正确;答案③中的两个平面 ![]() ,可以推出两个平面
,可以推出两个平面 ![]() 相交,故也不正确;对于答案④,可将直线n平移到到平面
相交,故也不正确;对于答案④,可将直线n平移到到平面 ![]() 内,借助异面直线平移后不相交的结论及面面平行的判定定理可知
内,借助异面直线平移后不相交的结论及面面平行的判定定理可知 ![]() ,是正确命题, 所以答案是:A。
,是正确命题, 所以答案是:A。
【考点精析】本题主要考查了直线与平面平行的判定和直线与平面平行的性质的相关知识点,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行;简记为:线面平行则线线平行才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】在空间中,给出下面四个命题,则其中正确命题的个数为( )
①过平面 ![]() 外的两点,有且只有一个 平面与平面
外的两点,有且只有一个 平面与平面 ![]() 垂直;
垂直;
②若平面 ![]() 内有不共线三点到平面
内有不共线三点到平面 ![]() 的距离都相等,则
的距离都相等,则 ![]() ∥
∥ ![]() ;
;
③若直线 ![]() 与平面内的无数条直线垂直,则
与平面内的无数条直线垂直,则 ![]() ;
;
④两条异面直线在同一平面内的射影一定是两平行线;
A.3
B.2
C.1
D.0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产一种机器的固定成本为0.5万元,但每生产1百台时,又需可变成本(即另增加投入)0.25万元.市场对此商品的年需求量为5百台,销售的收入(单位:万元)函数为:R(x)=5x﹣ ![]() x2(0≤x≤5),其中x是产品生产的数量(单位:百台).
x2(0≤x≤5),其中x是产品生产的数量(单位:百台).
(1)将利润表示为产量的函数;
(2)年产量是多少时,企业所得利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,2(a2﹣b2)=2accosB+bc. (Ⅰ)求A;
(Ⅱ)D为边BC上一点,BD=3DC,∠DAB= ![]() ,求tanC.
,求tanC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】和谐高级中学共有学生570名,各班级人数如表:
一班 | 二班 | 三班 | 四班 | |
高一 | 52 | 51 | y | 48 |
高二 | 48 | x | 49 | 47 |
高三 | 44 | 47 | 46 | 43 |
已知在全校学生中随机抽取1名,抽到高二年级学生的概率是 ![]() .
.
(1)求x,y的值;
(2)现用分层抽样的方法在全校抽取114名学生,应分别在各年级抽取多少名?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,平面ABCD⊥平面ABEF,四边形ABCD是正方形,四边形ABEF是矩形,且AF= ![]() AD=a,G是EF的中点,则GB与平面AGC所成角的正弦值为( )
AD=a,G是EF的中点,则GB与平面AGC所成角的正弦值为( ) 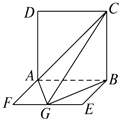
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某圆拱桥的示意图如图所示,该圆拱的跨度AB是36 m,拱高OP是6 m,在建造时,每隔3 m需用一个支柱支撑,求支柱A2P2的长.(精确到0.01 m)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:关于x的不等式x2+(a﹣1)x+1≤0的解集为;命题q:方程 ![]() 表示焦点在y轴上的椭圆;若命题q为真命题,p∨q为真命题.
表示焦点在y轴上的椭圆;若命题q为真命题,p∨q为真命题.
(1)求实数a的取值范围;
(2)判断方程(a+1)x2+(1﹣a)y2=(a+1)(1﹣a)所表示的曲线的形状.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年12月1日,汉孝城际铁路正式通车运营.除始发站(汉口站)与终到站(孝感东站)外,目前沿途设有7个停靠站,其中,武汉市辖区内有4站(后湖站、金银潭站、天河机场站、天河街站),孝感市辖区内有3站(闵集站、毛陈站、槐荫站).为了了解该线路运营状况,交通管理部门计划从这7个车站中任选3站调研.
(1)求孝感市辖区内至少选中1个车站的概率;
(2)若孝感市辖区内共选中了X个车站,求随机变量X的分布列与期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com