
【题目】直角坐标系xOy中,点A坐标为(2,0),点B坐标为(4,3),点C坐标为(1,3),且![]() (t∈R).
(t∈R).

(1) 若CM⊥AB,求t的值;
(2) 当0≤ t ≤1时,求直线CM的斜率k和倾斜角θ的取值范围.
科目:高中数学 来源: 题型:
【题目】设圆C1:x2+y2﹣10x+4y+25=0与圆C2:x2+y2﹣14x+2y+25=0,点A,B分别是C1,C2上的动点,M为直线y=x上的动点,则|MA|+|MB|的最小值为( )
A.3![]() B.3
B.3![]() C.5
C.5![]() D.5
D.5![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义区间![]() ,
,![]() ,
,![]() ,
,![]() 的长度均为
的长度均为![]() ,其中
,其中![]() .
.
(1)已知函数![]() 的定义域为
的定义域为![]() ,值域为
,值域为![]() ,写出区间
,写出区间![]() 长度的最大值与最小值.
长度的最大值与最小值.
(2)已知函数![]() 的定义域为实数集
的定义域为实数集![]() ,满足
,满足![]() (
(![]() 是
是![]() 的非空真子集).集合
的非空真子集).集合![]() ,
,![]() ,求
,求![]() 的值域所在区间长度的总和.
的值域所在区间长度的总和.
(3)定义函数![]() ,判断函数
,判断函数![]() 在区间
在区间![]() 上是否有零点,并求不等式
上是否有零点,并求不等式![]() 解集区间的长度总和.
解集区间的长度总和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大型工厂招聘到一大批新员工.为了解员工对工作的熟练程度,从中随机抽取100人组成样本,统计他们每天加工的零件数,得到如下数据:

将频率作为概率,解答下列问题:
(1)当![]() 时,从全体新员工中抽取2名,求其中恰有1名日加工零件数达到240及以上的概率;
时,从全体新员工中抽取2名,求其中恰有1名日加工零件数达到240及以上的概率;
(2)若根据上表得到以下频率分布直方图,估计全体新员工每天加工零件数的平均数为222个,求![]() 的值(每组数据以中点值代替);
的值(每组数据以中点值代替);

(3)在(2)的条件下,工厂按工作熟练度将新员工分为三个等级:日加工零件数未达200的员工为C级;达到200但未达280的员工为B级;其他员工为A级.工厂打算将样本中的员工编入三个培训班进行全员培训:A,B,C三个等级的员工分别参加高级、中级、初级培训班,预计培训后高级、中级、初级培训班的员工每人的日加工零件数分别可以增加20,30,50.现从样本中随机抽取1人,其培训后日加工零件数增加量为X,求随机变量X的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,一块黄铜板上插着三根宝石针,在其中一根针上从下到上穿好由大到小的若干金片.若按照下面的法则移动这些金片:每次只能移动一片金片;每次移动的金片必须套在某根针上;大片不能叠在小片上面.设移完n片金片总共需要的次数为an,可推得a1=1,an+1=2an+1.如图是求移动次数在1000次以上的最小片数的程序框图模型,则输出的结果是( )

A. 8B. 9C. 10D. 11
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为了了解高中生的艺术素养,从学校随机选取男,女同学各50人进行研究,对这100名学生在音乐、美术、戏剧、舞蹈等多个艺术项目进行多方位的素质测评,并把调查结果转化为个人的素养指标![]() 和
和![]() ,制成下图,其中“*”表示男同学,“+”表示女同学.
,制成下图,其中“*”表示男同学,“+”表示女同学.

若![]() ,则认定该同学为“初级水平”,若
,则认定该同学为“初级水平”,若![]() ,则认定该同学为“中级水平”,若
,则认定该同学为“中级水平”,若![]() ,则认定该同学为“高级水平”;若
,则认定该同学为“高级水平”;若![]() ,则认定该同学为“具备一定艺术发展潜质”,否则为“不具备明显艺术发展潜质”.
,则认定该同学为“具备一定艺术发展潜质”,否则为“不具备明显艺术发展潜质”.
(I)从50名女同学的中随机选出一名,求该同学为“初级水平”的概率;
(Ⅱ)从男同学所有“不具备明显艺术发展潜质的中级或高级水平”中任选2名,求选出的2名均为“高级水平”的概率;
(Ⅲ)试比较这100名同学中,男、女生指标![]() 的方差的大小(只需写出结论).
的方差的大小(只需写出结论).
查看答案和解析>>
科目:高中数学 来源: 题型:
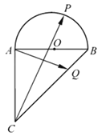
【题目】如图,在等腰直角三角形ABC中,∠CAB=90°,AB=2,以AB为直径在△ABC外作半圆O,P为半圆弧AB上的动点,点Q在斜边BC上,若![]() =
=![]() ,则
,则![]() 的最小值为_______.
的最小值为_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com