
【题目】等比数列{an}的各项均为正数,且2a3是a2与a6的等比中项,2a1+3a2=16.
(1)求数列{an}的通项公式;
(2)设bn=log2a1+log2a2+…+log2an , 求数列{ ![]() }的前n项和Sn .
}的前n项和Sn .
【答案】
(1)解:设等比数列{an}的公比为q>0,∵2a3是a2与a6的等比中项,2a1+3a2=16.
∴ ![]() =a2a6,即
=a2a6,即 ![]() =
= ![]() ,a1(2+3q)=16,
,a1(2+3q)=16,
解得a1=q=2,
∴an=2n.
(2)解:bn=log2a1+log2a2+…+log2an= ![]() =
= ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() =2
=2 ![]() .
.
∴数列{ ![]() }的前n项和Sn=2
}的前n项和Sn=2 ![]() +…+
+…+ ![]()
=2 ![]()
= ![]()
【解析】(1)利用等比数列的通项公式即可得出.(2)利用对数的运算性质、等差数列的求和公式可得bn , 再利用“裂项求和”方法即可得出.
【考点精析】掌握等比数列的通项公式(及其变式)和等比数列的前n项和公式是解答本题的根本,需要知道通项公式:![]() ;前
;前![]() 项和公式:
项和公式: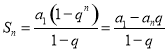 .
.


科目:高中数学 来源: 题型:
【题目】如图![]() 是某公共汽车线路收支差额
是某公共汽车线路收支差额![]() 元与乘客量
元与乘客量![]() 的图象.由于目前本条线路亏损,公司有关人员提出了两种扭亏为赢的方案,根据图
的图象.由于目前本条线路亏损,公司有关人员提出了两种扭亏为赢的方案,根据图![]() 上点
上点![]() 、点
、点![]() 以及射线
以及射线![]() 上的点的实际意义,用文字说明图
上的点的实际意义,用文字说明图![]() 方案是______,图
方案是______,图![]() 方案是______.
方案是______.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).在以原点
为参数).在以原点![]() 为极点,
为极点,![]() 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给定椭圆![]() ,称圆
,称圆![]() 为椭圆
为椭圆![]() 的“伴随圆”.已知点
的“伴随圆”.已知点![]() 是椭圆
是椭圆![]() 上的点
上的点
(1)若过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 有且只有一个公共点,求
有且只有一个公共点,求![]() 被椭圆
被椭圆![]() 的伴随圆
的伴随圆![]() 所截得的弦长:
所截得的弦长:
(2)![]() 是椭圆
是椭圆![]() 上的两点,设
上的两点,设![]() 是直线
是直线![]() 的斜率,且满足
的斜率,且满足![]() ,试问:直线
,试问:直线![]() 是否过定点,如果过定点,求出定点坐标,如果不过定点,试说明理由。
是否过定点,如果过定点,求出定点坐标,如果不过定点,试说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】自2016年1月1日起,我国全面二孩政策正式实施,这次人口与生育政策的历史性调整,使得“要不要再生一个”“生二孩能休多久产假”等成为千千万万个家庭在生育决策上避不开的话题.为了解针对产假的不同安排方案形成的生育意愿,某调查机构随机抽取了200户有生育二胎能力的适龄家庭进行问卷调查,得到如下数据:
产假安排(单位:周) | 14 | 15 | 16 | 17 | 18 |
有生育意愿家庭数 | 4 | 8 | 16 | 20 | 26 |
(1)若用表中数据所得的频率代替概率,面对产假为14周与16周,估计某家庭有生育意愿的概率分别为多少?
(2)假设从5种不同安排方案中,随机抽取2种不同安排分别作为备选方案,然后由单位根据单位情况自主选择.
①求两种安排方案休假周数和不低于32周的概率;
②如果用ξ表示两种方案休假周数和.求随机变量ξ的分布及期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,共享单车已经悄然进入了广大市民的日常生活,并慢慢改变了人们的出行方式.为了更好地服务民众,某共享单车公司在其官方![]() 中设置了用户评价反馈系统,以了解用户对车辆状况和优惠活动的评价.现从评价系统中选出
中设置了用户评价反馈系统,以了解用户对车辆状况和优惠活动的评价.现从评价系统中选出![]() 条较为详细的评价信息进行统计,车辆状况的优惠活动评价的
条较为详细的评价信息进行统计,车辆状况的优惠活动评价的![]() 列联表如下:
列联表如下:
对优惠活动好评 | 对优惠活动不满意 | 合计 | |
对车辆状况好评 |
|
|
|
对车辆状况不满意 |
|
|
|
合计 |
|
|
|
(1)能否在犯错误的概率不超过![]() 的前提下认为优惠活动好评与车辆状况好评之间有关系?
的前提下认为优惠活动好评与车辆状况好评之间有关系?
(2)为了回馈用户,公司通过![]() 向用户随机派送骑行券.用户可以将骑行券用于骑行付费,也可以通过
向用户随机派送骑行券.用户可以将骑行券用于骑行付费,也可以通过![]() 转赠给友.某用户共获得了
转赠给友.某用户共获得了![]() 张骑行券,其中只有
张骑行券,其中只有![]() 张是一元券.现该用户从这
张是一元券.现该用户从这![]() 张骑行券中随机选取
张骑行券中随机选取![]() 张转赠给好友,求选取的
张转赠给好友,求选取的![]() 张中至少有
张中至少有![]() 张是一元券的概率.
张是一元券的概率.
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
参考公式:![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班准备从甲、乙、丙等6人中选出4人参加某项活动,要求甲、乙、丙三人中至少有两人参加,那么不同的方法有 ( )
A. 18种 B. 12种 C. 432种 D. 288种
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com