
【题目】已知P(﹣2,3)是函数y= ![]() 图象上的点,Q是双曲线在第四象限这一分支上的动点,过点Q作直线,使其与双曲线y=
图象上的点,Q是双曲线在第四象限这一分支上的动点,过点Q作直线,使其与双曲线y= ![]() 只有一个公共点,且与x轴、y轴分别交于点C、D,另一条直线y=
只有一个公共点,且与x轴、y轴分别交于点C、D,另一条直线y= ![]() x+6与x轴、y轴分别交于点A、B.则
x+6与x轴、y轴分别交于点A、B.则
(1)O为坐标原点,三角形OCD的面积为 .
(2)四边形ABCD面积的最小值为 .
【答案】
(1)12
(2)48
【解析】解:(1.)∵P(﹣2,3)是函数y= ![]() 图象上的点, 故k=﹣6,即y=
图象上的点, 故k=﹣6,即y= ![]() ,则y′=
,则y′= ![]() ,
,
设Q是双曲线在第四象限这一分支上的动点(a, ![]() ),(a>0),
),(a>0),
则由题意得直线CD与双曲线在第四象限这一分支相切,
故直线CD的方程为:y+ ![]() =
= ![]() (x﹣a),
(x﹣a),
令y=0,可得x=2a,即C点坐标为(2a,0),
令x=0,可得y=﹣ ![]() ,即D点坐标为(0,﹣
,即D点坐标为(0,﹣ ![]() ),
),
故三角形OCD的面积S△OCD= ![]() ×2a×
×2a× ![]() =12,
=12,
(2.)∵直线y= ![]() x+6与x轴、y轴分别交于点A、B,
x+6与x轴、y轴分别交于点A、B,
则A(﹣4,0),B(0,6),
故四边形ABCD面积S=S△OAB+S△OBC+S△OCD+S△OAD= ![]() ×4×6+
×4×6+ ![]() ×2a×6+
×2a×6+ ![]() ×4×
×4× ![]() +12=24+6a+
+12=24+6a+ ![]() ≥24+2
≥24+2 ![]() =48,
=48,
即四边形ABCD面积的最小值为48,
所以答案是:12,48
【考点精析】解答此题的关键在于理解函数的最值及其几何意义的相关知识,掌握利用二次函数的性质(配方法)求函数的最大(小)值;利用图象求函数的最大(小)值;利用函数单调性的判断函数的最大(小)值.


科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中直线
中直线![]() 的倾斜角为
的倾斜角为![]() ,且经过点
,且经过点![]() ,以坐标系
,以坐标系![]() 的原点为极点,
的原点为极点, ![]() 轴的非负半轴为极轴,建立极坐标系
轴的非负半轴为极轴,建立极坐标系![]() ,曲线
,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,过点
两点,过点![]() 的直线
的直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,且
两点,且![]() .
.
(1)平面直角坐标系中,求直线![]() 的一般方程和曲线
的一般方程和曲线![]() 的标准方程;
的标准方程;
(2)求证: ![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的准线为
的准线为![]() ,焦点为
,焦点为![]() ,
, ![]() 为坐标原点.
为坐标原点.
(1)求过点![]() ,且与
,且与![]() 相切的圆的方程;
相切的圆的方程;
(2)过![]() 的直线交抛物线
的直线交抛物线![]() 于
于![]() 两点,
两点, ![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,求证:直线
,求证:直线![]() 过定点.
过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,矩形ABCD和梯形BEFC所在平面互相垂直,∠BCF=∠CEF=90°,AD= ![]() .
.
(Ⅰ)求证:AE∥平面DCF;
(Ⅱ)当AB的长为何值时,二面角A﹣EF﹣C的大小为60°?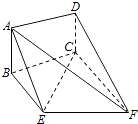
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知x,y满足约束条件 ![]() ,当目标函数z=ax+by(a>0,b>0)在该约束条件下取到最小值2
,当目标函数z=ax+by(a>0,b>0)在该约束条件下取到最小值2 ![]() 时,a2+b2的最小值为( )
时,a2+b2的最小值为( )
A.5
B.4
C.![]()
D.2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着生活水平的提高,人们对空气质量的要求越来越高,某机构为了解公众对“车辆限行”的态度,随机抽查![]() 人,并将调查情况进行整理后制成下表:
人,并将调查情况进行整理后制成下表:
年龄(岁) |
|
|
|
|
|
频数 |
|
|
|
|
|
赞成人数 |
|
|
|
|
|
(1)完成被调查人员年龄的频率分布直方图,并求被调査人员中持赞成态度人员的平均年龄约为多少岁?
(2)若从年龄在![]() 的被调查人员中各随机选取
的被调查人员中各随机选取![]() 人进行调查.请写出所有的基本亊件,并求选取
人进行调查.请写出所有的基本亊件,并求选取![]() 人中恰有
人中恰有![]() 人持不赞成态度的概率.
人持不赞成态度的概率.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com