
【题目】2012年,在“杂交水稻之父”袁隆平的实验田内种植了![]() ,
,![]() 两个品种的水稻,为了筛选出更优的品种,在
两个品种的水稻,为了筛选出更优的品种,在![]() ,
,![]() 两个品种的实验田中分别抽取7块实验田,如图所示的茎叶图记录了这14块实验田的亩产量(单位:
两个品种的实验田中分别抽取7块实验田,如图所示的茎叶图记录了这14块实验田的亩产量(单位:![]() ),通过茎叶图比较两个品种的均值及方差,并从中挑选一个品种进行以后的推广,有如下结论:①
),通过茎叶图比较两个品种的均值及方差,并从中挑选一个品种进行以后的推广,有如下结论:①![]() 品种水稻的平均产量高于
品种水稻的平均产量高于![]() 品种水稻,推广
品种水稻,推广![]() 品种水稻;②
品种水稻;②![]() 品种水稻的平均产量高于
品种水稻的平均产量高于![]() 品种水稻,推广
品种水稻,推广![]() 品种水稻;③
品种水稻;③![]() 品种水稻比
品种水稻比![]() 品种水稻产量更稳定,推广
品种水稻产量更稳定,推广![]() 品种水稻;④
品种水稻;④![]() 品种水稻比
品种水稻比![]() 品种水稻产量更稳定,推广
品种水稻产量更稳定,推广![]() 品种水稻;其中正确结论的编号为( )
品种水稻;其中正确结论的编号为( )

A.①②B.①③C.②④D.①④
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn,且Sn=2an﹣2(n∈N*),数列{bn}满足bn=(2n﹣1)an,数列{bn}的前n项和Tn(n∈N*),
(1)求数列{an}和{bn}的通项公式;
(2)求数列{bn}的前n项和Tn;
(3)求![]() 的最小值以及取得最小值时n的值.
的最小值以及取得最小值时n的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大型企业针对改善员工福利的![]() ,
,![]() ,
,![]() 三种方案进行了问卷调查,调查结果如下:
三种方案进行了问卷调查,调查结果如下:
支持 | 支持 | 支持 | |
35岁以下的人数 | 200 | 400 | 800 |
35岁及以上的人数 | 100 | 100 | 400 |
(1)从所有参与调查的人中,用分层随机抽样的方法抽取![]() 人,已知从支持
人,已知从支持![]() 方案的人中抽取了6人,求
方案的人中抽取了6人,求![]() 的值.
的值.
(2)从支持![]() 方案的人中,用分层随机抽样的方法抽取5人,这5人中年龄在35岁及以上的人数是多少?年龄在35岁以下的人数是多少?
方案的人中,用分层随机抽样的方法抽取5人,这5人中年龄在35岁及以上的人数是多少?年龄在35岁以下的人数是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的最小正周期为
的最小正周期为![]() ,图象过点
,图象过点![]() .
.
(1)求![]() 、
、![]() 的值和
的值和![]() 的单调增区间;
的单调增区间;
(2)将函数![]() 的图象向右平移
的图象向右平移![]() 个单位,再将图象上各点的横坐标伸长到原来的2倍(纵坐标不变),得到函数
个单位,再将图象上各点的横坐标伸长到原来的2倍(纵坐标不变),得到函数![]() 的图象,若函数
的图象,若函数![]() 在区间
在区间![]() 上有且只有两个不同零点,求实数
上有且只有两个不同零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,点
,点![]() 为圆
为圆![]() 上任意一点,点
上任意一点,点![]() ,线段
,线段![]() 的中点为
的中点为![]() ,点
,点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)直线![]() 与圆
与圆![]() 相交于
相交于![]() 两点,求
两点,求![]() 的最小值及此时直线
的最小值及此时直线![]() 的方程;
的方程;
(3)求曲线![]() 与
与![]() 的公共弦长.
的公共弦长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了丰富学生的课外文化生活,某中学积极探索开展课外文体活动的新途径及新形式,取得了良好的效果.为了调查学生的学习积极性与参加文体活动是否有关,学校对200名学生做了问卷调查,列联表如下:
参加文体活动 | 不参加文体活动 | 合计 | |
学习积极性高 | 80 | ||
学习积极性不高 | 60 | ||
合计 | 200 |
已知在全部200人中随机抽取1人,抽到学习积极性不高的学生的概率为![]() .
.
(1)请将上面的列联表补充完整;
(2)是否有99.9%的把握认为学习积极性高与参加文体活动有关?请说明你的理由;
(3)若从不参加文体活动的同学中按照分层抽样的方法选取5人,再从所选出的5人中随机选取2人,求至少有1人学习积极性不高的概率.
附:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
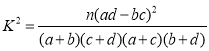 ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对平面区域![]() ,用
,用![]() 表示属于
表示属于![]() 的所有整点(即
的所有整点(即![]() 平面上坐标
平面上坐标![]() 都是整数的点)的个数.若
都是整数的点)的个数.若![]() 表示由曲线
表示由曲线![]() 和两直线
和两直线![]() 所围成的区域(包括边界);
所围成的区域(包括边界);![]() 表示由曲线
表示由曲线![]() 和两直线
和两直线![]() 所围成的区域(包括边界).则
所围成的区域(包括边界).则![]() ______.
______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com