
【题目】下表提供了某厂节能降耗技术改造后生产产品过程中记录的产量x(吨)与相应的生产能耗y(吨)标准煤的几组对照数据:
x | 3 | 4 | 5 | 6 |
y | 2.5 | 3 | 4 | 4.5 |
(1)求y关于x的线性回归方程;(已知 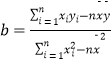 )
)
(2)已知该厂技术改造前100吨甲产品能耗为90吨标准煤,试根据(1)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技术改造前降低了多少吨标准煤.
【答案】
(1)解:∵ ![]() (吨),
(吨),
![]() (吨),
(吨),
![]() ,
,
![]() ,
,
∴ 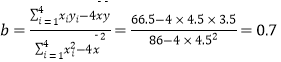 ,
,
∴a= ![]() ﹣0.7×
﹣0.7× ![]() =3.5﹣0.7×4.5=0.35,
=3.5﹣0.7×4.5=0.35,
∴y关于x的回归方程为 ![]()
(2)解:由(1)可知技术改造后100吨甲产品的生产能耗约为0.7×100+0.35=70.35(吨),
∵技术改造前100吨甲产品的生产能耗为90吨,
∴降低的能耗约为90﹣70.35=19.65(吨),
即预测生产100吨甲产品的生产能耗比技术改造前降低了19.65吨标准煤
【解析】(1)根据所给的这组数据求出利用最小二乘法所需要的几个数据,代入求系数b的公式,求得结果,再把样本中心点代入,求出a的值,得到线性回归方程.(2)根据上一问所求的线性回归方程,把x=100代入线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低标准煤的数量.


 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() sin
sin ![]() cos
cos ![]() +sin2
+sin2 ![]() (ω>0,0<φ<
(ω>0,0<φ< ![]() ).其图象的两个相邻对称中心的距离为
).其图象的两个相邻对称中心的距离为 ![]() ,且过点(
,且过点( ![]() ,1).
,1).
(1)函数f(x)的解析式;
(2)在△ABC中,角A,B,C所对的边分别为a,b,c.已知 ![]() =
= ![]() .且f(A)=
.且f(A)= ![]() ,求角C的大小.
,求角C的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足
满足![]() ,
, ![]() ,其中
,其中![]() .
.
(1)设![]() ,求证:数列
,求证:数列![]() 是等差数列,并求出
是等差数列,并求出![]() 的通项公式;
的通项公式;
(2)设![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,是否存在正整数
,是否存在正整数![]() ,使得
,使得![]() 对于
对于![]() 恒成立,若存在,求出
恒成立,若存在,求出![]() 的最小值,若不存在,请说明理由.
的最小值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某书店销售刚刚上市的某知名品牌的高三数学单元卷,按事先拟定的价格进行5天试销,每种单价试销1天,得到如下数据:
单价 | 18 | 19 | 20 | 21 | 22 |
销量 | 61 | 56 | 50 | 48 | 45 |
(1)求试销5天的销量的方差和![]() 对
对![]() 的回归直线方程;
的回归直线方程;
(2)预计今后的销售中,销量与单价服从(1)中的回归方程,已知每册单元卷的成本是14元,为了获得最大利润,该单元卷的单价卷的单价应定为多少元?
(附: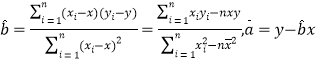 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题10分) 从3名男生和![]() 名女生中任选2人参加比赛。
名女生中任选2人参加比赛。
①求所选2人都是男生的概率;
②求所选2人恰有1名女生的概率;
③求所选2人中至少有1名女生的概率
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】解答
(1)在区间[1,3]上任取两整数a、b,求二次方程x2+2ax+b2=0有实数根的概率.
(2)在区间[1,3]上任取两实数a、b,求二次方程x2+2ax+b2=0有实数根的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近期中央电视台播出的《中国诗词大会》火遍全国,下面是组委会在选拔赛时随机抽取的100名选手的成绩,按成绩分组,得到的频率分布表如下所示:
组号 | 分组 | 频数 | 频率 |
第1组 |
|
| |
第2组 |
| ① | |
第3组 |
| 20 | ② |
第4组 |
| 20 |
|
第5组 |
| 10 |
|
合计 | 100 |
|
(1)请先求出频率分布表中①、②位置的相应数据,再完成频率分布直方图(用阴影表示);
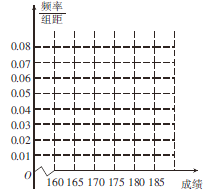
(2)为了能选拔出最优秀的选手,组委会决定在笔试成绩高的第3、4、5组中用分层抽样抽取5名选手进入第二轮面试,求第3、4、5组每组各抽取多少名选手进入第二轮面试;
(3)在(2)的前提下,组委会决定在5名选手中随机抽取2名选手接受![]() 考官进行面试,求:第4组至少有一名选手被考官
考官进行面试,求:第4组至少有一名选手被考官![]() 面试的概率.
面试的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(x+φ)(A>0,0<φ<π),x∈R的最大值是1,其图象经过点 ![]() .
.
(1)求f(x)的解析式;
(2)已知 ![]() ,且
,且 ![]() ,
, ![]() ,求f(α﹣β)的值.
,求f(α﹣β)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲,乙两台机床同时生产一种零件,其质量按测试指标划分:指标大于或等于100为优品,大于等于90且小于100为合格品,小于90为次品,现随机抽取这两台车床生产的零件各100件进行检测,检测结果统计如下:
测试指标 |
|
|
|
|
|
机床甲 | 8 | 12 | 40 | 32 | 8 |
机床乙 | 7 | 18 | 40 | 29 | 6 |
(1)试分别估计甲机床、乙机床生产的零件为优品的概率;
(2)甲机床生产一件零件,若是优品可盈利160元,合格品可盈利100元,次品则亏损20元;假设甲机床某天生产50件零件,请估计甲机床该天的日利润(单位:元);
(3)从甲、乙机床生产的零件指标在![]() 内的零件中,采用分层抽样的方法抽取5件,从这5件中任选2件进行质量分析,求这2件都是乙机床生产的概率.
内的零件中,采用分层抽样的方法抽取5件,从这5件中任选2件进行质量分析,求这2件都是乙机床生产的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com