
| A. | “b=0”是“函数f(x)=ax2+bx+c是偶函数”的充要条件. | |
| B. | 命题“存在x∈R,x2+x-1<0”的否定是“任意x∈R,x2+x-1>0” | |
| C. | 命题“在△ABC中,若A>B则sinA>sinB”的逆命题为假命题. | |
| D. | 函数y=f(x)为R上的可导函数,则f′(x0)=0是x0为函数f(x)极值点的充要条件. |
分析 根据偶函数的定义:f(-x)=f(x)判断A;由特称命题的否定判断B;由逆命题和正弦定理判断C;通过举特例和极值点的定义判断D.
解答 解:A、∵f(x)=ax2+bx+c为偶函数,∴f(-x)=a(-x)2+b(-x)+c=ax2-bx+c,
∴ax2-bx+c=ax2+bx+c,则b=0,
若b=0,则f(x)=ax2+bx+c=ax2+c=f(-x),
所以b=0是函数f(x)=ax2+bx+c为偶函数的充要条件,A正确;
B、命题“存在x∈R,x2+x-1<0”的否定是“任意x∈R,x2+x-1≥0”,B不正确;
C、“在△ABC中,若A>B则sinA>sinB”的逆命题是“在△ABC中,若sinA>sinB,则A>B”,
由正弦定理得,sinA>sinB⇒$\frac{a}{2R}>\frac{b}{2R}$⇒a>b⇒A>B,所以逆命题是真命题,C不正确;
D、如f(x)=x3,且f′(x)=3x2,但x=0不是函数的极值点,
则f′(x0)=0是x0为函数f(x)极值点的必要条件,D不正确,
故选:A.
点评 本题考查命题的真假判断,命题及其关系,充分条件与必要条件的判断,涉及的知识点较多,综合性强,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-1,0,1} | B. | {0,1} | C. | {0} | D. | {-1,0} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4$\sqrt{2}$ | B. | 2$\sqrt{2}$ | C. | 2$\sqrt{10}$ | D. | $\sqrt{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
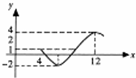 +c(A>0,ω>0,φ>0)图象的一部分.
+c(A>0,ω>0,φ>0)图象的一部分.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{3}}}{3}$ | B. | -$\sqrt{3}$ | C. | $\sqrt{3}$ | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 某高三学生进入高中三年来的第1次至14次数学考试成绩分别为:79,83,93,86,99,98,94,88,98,91,95,103,101,114,依次记为A1,A2…,A14.如图是成绩在一定范围内考试次数的一个算法流程图.那么输出的结果是( )
某高三学生进入高中三年来的第1次至14次数学考试成绩分别为:79,83,93,86,99,98,94,88,98,91,95,103,101,114,依次记为A1,A2…,A14.如图是成绩在一定范围内考试次数的一个算法流程图.那么输出的结果是( )| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com