
 ijУ�����꼶��ѧ��ĩ���е���������У�������ѧ�ɼ�������±���ʾ��
ijУ�����꼶��ѧ��ĩ���е���������У�������ѧ�ɼ�������±���ʾ��| ��ѧ�ɼ� | [90��105�� | [105��120�� | [120��135�� | [135��150] |
| �Ŀƿ��� | 57 | 40 | 24 | 6 |
| ���ƿ��� | 123 | x | y | z |
���� ��1�����ݷֲ���������ȡ�������������ɱ������ɵ���$\frac{1}{6}=\frac{5-1}{z}$���ɵ�z��
��2���ȼ����6����������ѧ�ɼ���ƽ�������������뷽�ʽ���ɵ�6����������ѧ�ɼ��ķ��
��3����У��ѧ�ɼ�������120�ֵ��Ŀ����ƿ�������֮��Ϊ1��3��������105�ֵ��Ŀ����ƿ�������֮��Ϊ2��5���ɵ�$\frac{24+6}{y+24}=\frac{1}{5}��\frac{40+24+6}{x+y+24}=\frac{2}{5}$����ⷽ����ɵ�x��y��ֵ��
��� �⣺��1��������$\frac{1}{6}=\frac{5-1}{z}$����z=24��
��2��$\overline{x}=\frac{135+135+136+138+140+144}{6}=138$��
��${s}^{2}=\frac{1}{6}$��[��135-138��2+��135-138��2+��136-138��2+��138-138��2+��140-138��2+��144-138��2=$\frac{1}{6}$��[32+32+22+02+22+62]=$\frac{31}{3}$��
��3��������$\frac{24+6}{y+24}=\frac{1}{5}��\frac{40+24+6}{x+y+24}=\frac{2}{5}$�����x=85��y=66��
��������ѧ��������Ϊ��123+85+66+24=298�ˣ�
���� ���⿼���֪ʶ���Ƿ����Ҷͼ���ֲ��������ͳ�Ʋ��ֵļ��ۺ�Ӧ�ã��ѶȲ������ڻ������ͣ�


 ǧ�������������ĩ�����Ծ�����ϵ�д�
ǧ�������������ĩ�����Ծ�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | -1 | C�� | 3 | D�� | -3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | f��x��=cos��2x$+\frac{��}{3}$�� | B�� | f��x��=-cos��2x-$\frac{��}{6}$�� | C�� | f��x��=-sin��2x+$\frac{��}{6}$�� | D�� | f��x��=sin��2x-$\frac{��}{6}$�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��2��Ϊ���ڵ�ż���� | B�� | �Ԧ�Ϊ���ڵ�ż���� | ||
| C�� | ��2��Ϊ���ڵ��溯�� | D�� | �Ԧ�Ϊ���ڵ��溯�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� |  | B�� |  | C�� | 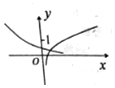 | D�� | 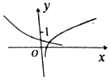 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com