
【题目】已知椭圆![]() 的两焦点为
的两焦点为![]() ,
, ![]() ,
, ![]() 为椭圆上一点,且到两个焦点的距离之和为6.
为椭圆上一点,且到两个焦点的距离之和为6.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若已知直线![]() ,当
,当![]() 为何值时,直线与椭圆
为何值时,直线与椭圆![]() 有公共点?
有公共点?
(3)若![]() ,求
,求![]() 的面积.
的面积.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)7.
;(3)7.
【解析】试题分析:(1)由焦点坐标得到c,由椭圆的定义求出a,进而求出b的值,即可得出椭圆的方程;(2)联立直线与椭圆方程,消去y, 直线与椭圆![]() 有公共点即所得一元二次方程有解,计算
有公共点即所得一元二次方程有解,计算![]() 得出m的范围;(3)
得出m的范围;(3) ![]() 中,
中, ![]() ,由勾股定理有
,由勾股定理有![]() ,结合椭圆的定义
,结合椭圆的定义![]() 代入化简可得
代入化简可得![]() ,根据三角形的面积公式求解即可.
,根据三角形的面积公式求解即可.
试题解析:
(1)∵椭圆的焦点是![]() 和
和![]() ,椭圆上一点到两个焦点的距离之和为6,
,椭圆上一点到两个焦点的距离之和为6,
∴设所求的椭圆方程为![]() ,
,
∴依题意有![]() ,
, ![]() ,∴
,∴![]() ,
,
∴所求的椭圆方程为![]() .
.
(2)由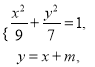 得
得![]() ,
,
由![]() 得
得![]() ,则
,则![]() ,
,
∴当![]() 时,直线与椭圆
时,直线与椭圆![]() 有公共点.
有公共点.
(3)∵点![]() 是椭圆
是椭圆![]() 上一点,
上一点,
∴由椭圆定义有![]() ,①
,①
又![]() 中,
中, ![]() ,
,
∴由勾股定理有![]() ,即
,即![]() ,②
,②
①2 ![]() ②,得
②,得![]() ,
,
∴![]() .
.


 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
已知直线l的参数方程为 (t为参数),曲线C的参数方程为
(t为参数),曲线C的参数方程为 (θ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,点P的极坐标为
(θ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,点P的极坐标为![]() 。
。
(Ⅰ)求直线l以及曲线C的极坐标方程;
(Ⅱ)设直线l与曲线C交于A,B两点,求△PAB的面积。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4![]() 4:坐标系与参数方程
4:坐标系与参数方程
在直角坐标系![]() 中,已知直线l1:
中,已知直线l1: ![]() (
(![]() ,
, ![]() ),抛物线C:
),抛物线C:  (t为参数).以原点
(t为参数).以原点![]() 为极点,
为极点, ![]() 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系.
(Ⅰ)求直线l1 和抛物线C的极坐标方程;
(Ⅱ)若直线l1 和抛物线C相交于点A(异于原点O),过原点作与l1垂直的直线l2,l2和抛物线C相交于点B(异于原点O),求△OAB的面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知y=f(x)是定义在R上的偶函数,当x≥0时,f(x)=x2﹣2x.
(1)求f(x)的解析式;
(2)作出函数f(x)的图象,并指出其单调区间.(不需要严格证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角梯形![]() 中,
中, ![]() //
// ![]() ,
, ![]() ⊥
⊥![]() ,
, ![]() ⊥
⊥![]() , 点
, 点![]() 是
是![]() 边的中点, 将△
边的中点, 将△![]() 沿
沿![]() 折起,使平面
折起,使平面![]() ⊥平面
⊥平面![]() ,连接
,连接![]() ,
, ![]() ,
, ![]() , 得到如图所示的几何体.
, 得到如图所示的几何体.
(Ⅰ)求证: ![]() ⊥平面
⊥平面![]() ;
;
(Ⅱ)若![]() ,
, ![]() ,求二面角
,求二面角![]() 的大小.
的大小.


查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列各组函数f(x)与g(x)的图象相同的是( )
A.f(x)=x,g(x)=( ![]() )2
)2
B.f(x)=x2 , g(x)=(x+1)2
C.f(x)=1,g(x)=x0
D.f(x)=|x|,g(x)= ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com