练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】对任意实数给出下列命题:①“”是“”的充要条件;②“是无理数”是“是无理数”的充要条件;③“”是“”的充分条件;④“”是“”的必要条件.其中真命题的个数是(　　)

    A.1B.2C.3D.4

    【答案】B

    【解析】

    根据充要条件的定义对题目中的四个答案逐一进行分析即可得到答案．

    ∵①中“”“”为真命题，

    但当时，“” “”为假命题，

    故“”是“”的充分不必要条件，故①为假命题；

    ∵②中“是无理数”“是无理数”为真命题，

    “是无理数”“是无理数”也为真命题，

    故“是无理数”是“是无理数”的充要条件，故②为真命题；

    ∵③中“”“”为假命题，

    “”“”也为假命题，

    故“”是“”即不充分也不必要条件，故③为假命题；

    ∵④中，故“”是“”的必要条件，

    故④为真命题．故真命题的个数为2

    故选：B

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图是一“T”型水渠的平面视图（俯视图），水渠的南北方向和东西方向轴截面均为矩形，南北向渠宽为4m，东西向渠宽m（从拐角处，即图中，处开始）．假定渠内的水面始终保持水平位置（即无高度差）．

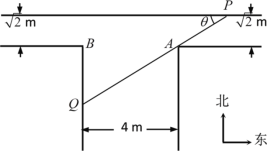
    （1）在水平面内，过点的一条直线与水渠的内壁交于，两点，且与水渠的一边的夹角为，将线段的长度表示为的函数；

    （2）若从南面漂来一根长为7m的笔直的竹竿（粗细不计），竹竿始终浮于水平面内，且不发生形变，问：这根竹竿能否从拐角处一直漂向东西向的水渠（不会卡住）？请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，.

    （1）若，求的最值；

    （2）若当时，，求m的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某校的一个社会实践调查小组，在对该校学生的良好“用眼习惯”的调查中，随机发放了120分问卷.对收回的100份有效问卷进行统计，得到如下列联表：

    做不到科学用眼

    能做到科学用眼

    合计

    男

    45

    10

    55

    女

    30

    15

    45

    合计

    75

    25

    100

    （1）现按女生是否能做到科学用眼进行分层，从45份女生问卷中抽取了6份问卷，从这6份问卷中再随机抽取3份，并记其中能做到科学用眼的问卷的份数，试求随机变量的分布列和数学期望；

    （2）若在犯错误的概率不超过的前提下认为良好“用眼习惯”与性别有关，那么根据临界值表，最精确的的值应为多少？请说明理由.

    附：独立性检验统计量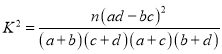，其中.

    独立性检验临界值表：

    0.25

    0.15

    0.10

    0.05

    0.025

    1.323

    2.072

    2.706

    3.840

    5.024

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某中学某社团为研究高三学生课下钻研数学时间与数学考试中的解答题得分的关系，随机调查了某中学高三某班名学生每周课下钻研数学时间(单位：小时)与高三下学期期中考试数学解答题得分，数据如下表：

    2

    4

    6

    8

    10

    12

    30

    38

    44

    48

    50

    54

    （1）根据上述数据，求出数学考试中的解答题得分与该学生课下钻研数学时间的线性回归方程，并预测某学生每周课下钻研数学时间为小时其数学考试中的解答题得分；

    （2）从这人中任选人，求人中至少有人课下钻研数学时间不低于小时的概率.

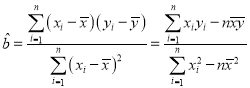    参考公式：，其中， ；参考数据：

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知8支球队中有3支弱队，以抽签方式将这8支球队分为A、B两组，每组4支．求：（1）A、B两组中有一组恰有两支弱队的概率；

    （2）A组中至少有两支弱队的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某运输公司每天至少向某地运送物质，该公司有8辆载重为的型卡车与4辆载重为的型卡车，有10名驾驶员，每辆卡车每天往返的次数为型卡车4次，型卡车3次；每辆卡车每天往返的成本为型卡车320元，型卡车504元，你认为该公司怎样调配车辆，使运费成本最低，最低运费是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】甲、乙两人各射击一次，击中目标的概率分别是和，假设两人射击是否击中目标，相互之间没有影响；每次射击是否击中目标，相互之间没有影响．

    （1）求甲射击4次，至多1次未击中目标的概率；

    （2）求两人各射击4次，甲恰好击中目标2次且乙恰好击中目标3次的概率；

    （3）假设某人连续2次未击中目标，则停止射击，求乙恰好射击5次后被中止射击的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】有4位同学在同一天的上午、下午参加“身高与体重”“立定跳远”“肺活量”“握力”“台阶”5个项目的测试，每位同学上午、下午各测试1个项目，且不重复.若上午不测“握力”项目，下午不测“台阶”项目，其余项目上午、下午都各测试1人，则不同的安排方式有多少种？

    查看答案和解析>>

    同步练习册答案