
【题目】如图,直三棱柱ABC﹣A1B1C1中,AA1=AB=AC=2,D,E,F分别是B1A1 , CC1 , BC的中点,AE⊥A1B1 , D为棱A1B1上的点. 
(1)证明:DF⊥AE;
(2)求平面DEF与平面ABC所成锐二面角的余弦值.
【答案】
(1)证明:∵AE⊥A1B1,A1B1∥AB,
∴AB⊥AE,又∵AB⊥AA1,AE∩AA1=A,
∴AB⊥面A1ACC1,又∵AC面A1ACC1,
∴AB⊥AC,
以A为原点,分别以AB,AC,AA1所在直线为x,y,z轴,
建立空间直角坐标系,
则A(0,0,0),E(0,2,1),F(1,1,0),A1(0,0,2),B1(2,0,2),
设D(x,y,z), ![]() =λ
=λ ![]() ,且λ∈[0,1],
,且λ∈[0,1],
即(x,y,z﹣2)=λ(2,0,0),∴D(2λ,0,2),
∴ ![]() =(1﹣2λ,1,﹣2),
=(1﹣2λ,1,﹣2), ![]() =(0,2,1),
=(0,2,1),
∵ ![]() =0+2﹣2=0,
=0+2﹣2=0,
∴DF⊥AE
(2)解: D(1,0,2),E(0,2,1),F(1,1,1),
![]() =(﹣1,2,﹣1),
=(﹣1,2,﹣1), ![]() =(0,1,﹣1),
=(0,1,﹣1),
设平面DEF的法向量 ![]() =(x,y,z),
=(x,y,z),
则  ,取y=1,得
,取y=1,得 ![]() =(1,1,1),
=(1,1,1),
平面ABC的法向量 ![]() =(0,0,1),
=(0,0,1),
cos< ![]() >=
>= ![]() =
= ![]() .
.
∴平面DEF与平面ABC所成锐二面角的余弦值为 ![]() .
.

【解析】(1)推导出AB⊥AE,AB⊥AA1 , 从而AB⊥面A1ACC1 , 由此能证明AB⊥AC,以A为原点,分别以AB,AC,AA1所在直线为x,y,z轴,建立空间直角坐标系,利用向量法能证明DF⊥AE.(2)求出平面DEF的法向量和平面ABC的法向量,利用向量法能求出平面DEF与平面ABC所成锐二面角的余弦值.
【考点精析】解答此题的关键在于理解空间中直线与直线之间的位置关系的相关知识,掌握相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点.


科目:高中数学 来源: 题型:
【题目】我国古代著名的![]() 周髀算经
周髀算经![]() 中提到:凡八节二十四气,气损益九寸九分六分分之一;冬至晷
中提到:凡八节二十四气,气损益九寸九分六分分之一;冬至晷![]() 长一丈三尺五寸,夏至晷长一尺六寸
长一丈三尺五寸,夏至晷长一尺六寸![]() 意思是:一年有二十四个节气,每相邻两个节气之间的日影长度差为
意思是:一年有二十四个节气,每相邻两个节气之间的日影长度差为![]() 分;且“冬至”时日影长度最大,为1350分;“夏至”时日影长度最小,为160分
分;且“冬至”时日影长度最大,为1350分;“夏至”时日影长度最小,为160分![]() 则“立春”时日影长度为
则“立春”时日影长度为![]()
![]()

A. ![]() 分B.
分B. ![]() 分C.
分C. ![]() 分D.
分D. ![]() 分
分
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校200名学生的数学期中考试成绩频率分布直方图如图所示,其中成绩分组区间是![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.

(1)求图中![]() 的值;
的值;
(2)根据频率分布直方图,估计这200名学生的平均分;
(3)若这200名学生的数学成绩中,某些分数段的人数![]() 与英语成绩相应分数段的人数
与英语成绩相应分数段的人数![]() 之比如下表所示,求英语成绩在
之比如下表所示,求英语成绩在![]() 的人数.
的人数.
分数段 |
|
|
|
|
|
| 1:2 | 2:1 | 6:5 | 1:2 | 1:1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某小区抽取100户居民进行月用电量调查,发现其用电量都在50度至350度之间,频率分布直方图如图所示. 
(1)根据直方图求x的值,并估计该小区100户居民的月均用电量(同一组中的数据用该组区间的中点值作代表);
(2)从该小区已抽取的100户居民中,随机抽取月用电量超过250度的3户,参加节约用电知识普及讲座,其中恰有ξ户月用电量超过300度,求ξ的分布列及期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某实验单次成功的概率为0.8,记事件A为“在实验条件相同的情况下,重复3次实验,各次实验互不影响,则3次实验中至少成功2次”,现采用随机模拟的方法估计事件4的概率:先由计算机给出0~9十个整数值的随机数,指定0,1表示单次实验失败,2,3,4,5,6,7,8,9表示单次实验成功,以3个随机数为组,代表3次实验的结果经随机模拟产生了20组随机数,如下表:
752 | 029 | 714 | 985 | 034 |
437 | 863 | 694 | 141 | 469 |
037 | 623 | 804 | 601 | 366 |
959 | 742 | 761 | 428 | 261 |
根据以上方法及数据,估计事件A的概率为( )
A.0.384B.0.65C.0.9D.0.904
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“微信运动”是腾讯开发的一个记录跑步或行走情况(步数里程)的公众号用户通过该公众号可查看自己某时间段的运动情况.某人根据2018年1月至2018年11月期间每月离步的里程(单位:十公里)的数据绘制了下面的折线图.根据该折线图,下列结论正确的是( )

A.月跑步里程逐月增加
B.月跑步里程最大值出现在10月
C.月跑步里程的中位数为5月份对应的里程数
D.1月至5月的月跑步里程相对于6月至11月波动性更小,变化比较平稳
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂新研发了一种产品,该产品每件成本为5元,将该产品按事先拟定的价格进行销售,得到如下数据:
单价 | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
销量 | 90 | 84 | 83 | 80 | 75 | 68 |
(1)求销量![]() (件)关于单价
(件)关于单价![]() (元)的线性回归方程
(元)的线性回归方程![]() ;
;
(2)若单价定为10元,估计销量为多少件;
(3)根据销量![]() 关于单价
关于单价![]() 的线性回归方程,要使利润
的线性回归方程,要使利润![]() 最大,应将价格定为多少?
最大,应将价格定为多少?
参考公式: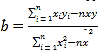 ,
,![]() .参考数据:
.参考数据:![]() ,
,![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com