
【题目】在平面直角坐标系xOy中,曲线C1的参数方程为![]() (α为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为
(α为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为![]() ,曲线C2的极坐标方程为
,曲线C2的极坐标方程为![]() (a>0).
(a>0).
(1)求直线l与曲线C1的交点的极坐标(ρ,θ)(ρ≥0,0≤θ<2π);
(2)若直线l与C2相切,求a的值.
科目:高中数学 来源: 题型:
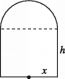
【题目】某制瓶厂要制造一批轴截面如图所示的瓶子,瓶子是按照统一规格设计的,瓶体上部为半球体,下部为圆柱体,并保持圆柱体的容积为3π.设圆柱体的底面半径为x,圆柱体的高为h,瓶体的表面积为S.
(1)写出S关于x的函数关系式;
(2)如何设计瓶子的尺寸(不考虑瓶壁的厚度),可以使表面积S最小,并求出最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在8件获奖作品中,有3件一等奖,有5件二等奖,从这8件作品中任取3件.
(1)求取出的3件作品中,一等奖多于二等奖的概率;
(2)设X为取出的3件作品中一等奖的件数,求随机变量X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一个口袋中装有n个红球(n≥1且n∈N+)和2个白球,从中有放回地连续摸三次,每次摸出2个球,若2个球颜色不同则为中奖,否则不中奖.
(1)当n=3时,设三次摸球中中奖的次数为X,求随机变量X的分布列;
(2)记三次摸球中恰有两次中奖的概率为P,求当n取多少时,P的值最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,BA,CD的延长线相交于点E,EF∥DA,并与CB的延长线交于点F,FG切⊙O于G.
(1)求证:BEEF=CEBF;
(2)求证:FE=FG.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),在以原点为极点,
为参数),在以原点为极点, ![]() 轴正半轴为极轴的极坐标系中,直线
轴正半轴为极轴的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的倾斜角;
的倾斜角;
(2)设点![]() ,直线
,直线![]() 和曲线
和曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经市场调查,某旅游城市在过去的一个月内(以30天计),第t天(1≤t≤30,t∈N*)的旅游人数f(t)(单位:万人)近似地满足f(t)=4+ ![]() ,而人均日消费俄g(t)(单位:元)近似地满足g(t)=
,而人均日消费俄g(t)(单位:元)近似地满足g(t)= ![]() .
.
(1)试求所有游客在该城市旅游的日消费总额W(t)(单位:万元)与时间t(1≤t≤30,t∈N*)的函数表达式;
(2)求所有游客在该城市旅游的日消费总额的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某海上养殖基地A,接到气象部门预报,位于基地南偏东60°方向相距20(![]() +1)海里的海面上有一台风中心,影响半径为20海里,正以每小时10
+1)海里的海面上有一台风中心,影响半径为20海里,正以每小时10![]() 海里的速度沿某一方向匀速直线前进,预计台风中心在基地东北方向时对基地的影响最强烈且(
海里的速度沿某一方向匀速直线前进,预计台风中心在基地东北方向时对基地的影响最强烈且(![]() +1)小时后开始影响基地持续2小时,求台风移动的方向.
+1)小时后开始影响基地持续2小时,求台风移动的方向.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有下列四个命题:
①“已知函数y=f(x),x∈ D,若D关于原点对称,则函数y=f(x),x∈ D为奇函数”的逆命题;
②“对应边平行的两角相等”的否命题;
③“若a≠0,则方程ax+b=0有实根”的逆否命题;
④“若A∪ B=B,则B≠A”的逆否命题.
其中的真命题是( )
A. ①② B. ②③
C. ①③ D. ③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com