分析:(1)以点D为坐标原点建立空间直角坐标系,要求直线CE与DB的夹角,代入向量夹角公式,可先求出
与
所成角的余弦,进而可求角
(2)可先设G的坐标,由AF⊥平面D
1EG,可知
⊥,⊥,利用向量的数量积的性质可求
解答: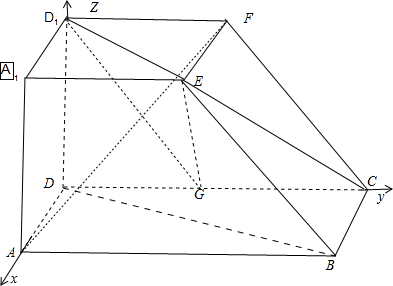
解:(1)以点D为坐标原点建立空间直角坐标系,设AB=2a,由AB=2AA
1=2A
1D
1=2A
1E.
可AB=2AA
1=2A
1D
1=2A
1E=2a,依题意得D(0,0,0),B(a,2a,0),C(0,2a,0),E(a,a,a)F(0,a,a),A(a,0,0),D
1(0,0,a)
∴
=(a,2a,0),
=(a,-a,a)
∴cos
<,>=
=
=
∴异面直线CE与DB所成的角为arccos
(2)证明:设G(0,m,0)易知
=(-a,a,a),
=(-a,m-a,-a),
=(-a,-a,0)∵AF⊥平面D
1EG,
∴
⊥,⊥,
∴
•=(-a)•(-a)+a(m-a)-a•a=0
∴m=a即G(0,a,0)
∴G为CD的中点时,满足AF⊥平面D
1EG,
点评:本题考查的知识点是用空间向量求异面直线间的夹角、直线与平面垂直的判定,用空间向量求直线的夹角,其中建立适当的空间坐标系,将空间线、面夹角问题转化为向量夹角问题是解答本题的关键.

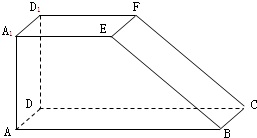 如图是长方体ABCD-A1B1C1D1被一个平面截去一部分后得到的几何体ABCD-A1EFD1,其中EF∥BC,且AB=2AA1=2A1D1=2A1E.
如图是长方体ABCD-A1B1C1D1被一个平面截去一部分后得到的几何体ABCD-A1EFD1,其中EF∥BC,且AB=2AA1=2A1D1=2A1E. 解:(1)以点D为坐标原点建立空间直角坐标系,设AB=2a,由AB=2AA1=2A1D1=2A1E.
解:(1)以点D为坐标原点建立空间直角坐标系,设AB=2a,由AB=2AA1=2A1D1=2A1E.

 如图在长方体ABCD-A1B1C1D1中,其中AB=BC,E,F分别是AB1,BC1的中点,则以下结论中
如图在长方体ABCD-A1B1C1D1中,其中AB=BC,E,F分别是AB1,BC1的中点,则以下结论中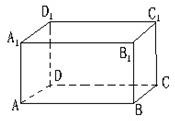 已知如图:长方体ABCD-A1B1C1D1中,交于顶点A的三条棱长别为AD=3,AA1=4,AB=5.一天,小强观察到在A处有一只蚂蚁,发现顶点C1处有食物,于是它沿着长方体的表面爬行去获取食物,则蚂蚁爬行的最短路程是( )
已知如图:长方体ABCD-A1B1C1D1中,交于顶点A的三条棱长别为AD=3,AA1=4,AB=5.一天,小强观察到在A处有一只蚂蚁,发现顶点C1处有食物,于是它沿着长方体的表面爬行去获取食物,则蚂蚁爬行的最短路程是( )