
设命题p:函数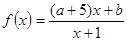 在(0,+
在(0,+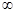 )上是增函数;命题q:方程
)上是增函数;命题q:方程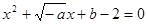 有两个不相等的负实数根,若p
有两个不相等的负实数根,若p q是真命题。
q是真命题。
(1)求点P(a,b)的轨迹图形的面积;
(2)求a+5b的取值范围。
(1) (2) (7,
(2) (7,  )
)
【解析】
试题分析:解:(1) f(x) =
f(x) = ,f ′(x)=
,f ′(x)=  ,
, p真
p真 x
x (0,+
(0,+ )时,
)时, >0
>0 a-b+5>0,(2′)
a-b+5>0,(2′) 方程x2+
方程x2+ x+b-2=0有两个不相等的负实数根
x+b-2=0有两个不相等的负实数根




 ,
,
即q真
 ;
5分
;
5分
若p q是真命题。则p真q真,
q是真命题。则p真q真,

 点P(a,b)的轨迹图形如图,
点P(a,b)的轨迹图形如图, ABC
ABC
的内部;(8′) 由边界可得A(0,2),B(-3,2),C(- ,
, )
)

 ABC的面积S=
ABC的面积S=
 3
3 (
( -2)=
-2)= ,
,
即点P(a,b)的轨迹图形的面积为 ;
10分
;
10分
(2)设a+5b="z," 直线a+5b=z过B点时,z=-3+5 2=7,直线a+5b=z过C点时,
2=7,直线a+5b=z过C点时,
z=- +5
+5
 =
= ,
, a+5b的取值范围是(7,
a+5b的取值范围是(7,  ) 13分
) 13分
考点:线性规划的运用
点评:解决的关键是能得到关于a,b的不等式组,然后作出可行域,结合图像来求解面积和最值,属于基础题。


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
命题P:![]() cn=0.
cn=0.
命题Q:当x∈[![]() ,2]时,函数f(x)=x+
,2]时,函数f(x)=x+![]() >
>![]() 恒成立.
恒成立.
如果P或Q为真命题,P且Q为假命题,求c的取值范围.
分析:由![]() cn=0得,0<c<1.∴P:0<c<1,
cn=0得,0<c<1.∴P:0<c<1,
由x∈[![]() ,2]时,函数f(x)=x+
,2]时,函数f(x)=x+![]() >
>![]() 恒成立,想到
恒成立,想到![]() <f(x)min,故需求f(x)在[
<f(x)min,故需求f(x)在[![]() ,2]上的最小值.
,2]上的最小值.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年河南省许昌市四校高三第一次联考数学卷 题型:解答题
(本小题满分12分)在a>0时,设命题p:函数y=ax在R上单调递增;命题q:不等式ax2-ax+1>0对x∈R恒成立,若p∧q为假,p∨q为真,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年四川省攀枝花市米易中学高三(上)第二次段考数学试卷(文科)(解析版) 题型:填空题
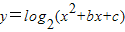 的值域为R
的值域为R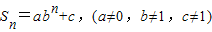 则此数列是等比数列的充要条件是a+c=0
则此数列是等比数列的充要条件是a+c=0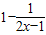 <0,命题q:-x 2+(2a+1)x-a(a+1)>0,若¬p是¬q的必要不充分条件,求实数a的取值范围0≤a≤
<0,命题q:-x 2+(2a+1)x-a(a+1)>0,若¬p是¬q的必要不充分条件,求实数a的取值范围0≤a≤ .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com