
分析 利用$\frac{1}{1+2+3+…+n}$=$\frac{2}{n(n+1)}$=2($\frac{1}{n}$-$\frac{1}{n+1}$),即可求极限.
解答 解:$\frac{1}{1+2+3+…+n}$=$\frac{2}{n(n+1)}$=2($\frac{1}{n}$-$\frac{1}{n+1}$),
∴$\underset{lim}{n→∞}$($\frac{1}{1+2}$+$\frac{1}{1+2+3}$+$\frac{1}{1+2+3+4}$+…+$\frac{1}{1+2+3+…+n}$)=$\underset{lim}{n→∞}$2($\frac{1}{2}-\frac{1}{n+1}$)=1,
故答案为1.
点评 本题考查极限的计算,考查等差数列的求和公式,属于中档题.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案科目:高中数学 来源: 题型:填空题
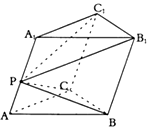 如图,P为三棱柱ABC-A1B1C1的侧棱AA1上的一个动点,若四棱锥P-BCC1B1的体积为V,则三棱柱ABC-A1B1C1的体积为$\frac{3}{2}V$(用V表示)
如图,P为三棱柱ABC-A1B1C1的侧棱AA1上的一个动点,若四棱锥P-BCC1B1的体积为V,则三棱柱ABC-A1B1C1的体积为$\frac{3}{2}V$(用V表示)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ¬p:?x∈R,x≤2 | B. | ¬p:?x∈R,x>2 | C. | ¬p:?x∈R,x>2 | D. | ¬p:?x∈R,x≤2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | b<a<c | B. | a>b>c | C. | a<b<c | D. | c<a<b |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1<k<$\frac{\sqrt{5}}{2}$ | B. | -$\frac{\sqrt{5}}{2}$<k<$\frac{\sqrt{5}}{2}$ | C. | -$\frac{\sqrt{5}}{2}$<k<-1 | D. | -$\frac{\sqrt{5}}{2}$<k<1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,+∞) | B. | (0,+∞) | C. | (0,1] | D. | $[{\frac{1}{2},1}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①③ | B. | ②③ | C. | ①② | D. | ①②③ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com