
【题目】在直角坐标系xOy中,以O为极点,x轴的非负半轴为极轴建立极坐标系,已知曲线C:ρsin2θ=2acosθ(a>0),l: 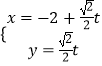 (t为参数)
(t为参数)
(1)求曲线C的普通方程,l的直角坐标方程
(2)设l与C交于M,N两点,点P(﹣2,0),若|PM|,|MN|,|PN|成等比数列,求实数a的值.
【答案】
(1)解:∵曲线C:ρsin2θ=2acosθ(a>0),∴ρ2sin2θ=2aρcosθ,(a>0),
∴曲线C的普通方程为y2=2ax,(a>0);
∵l的参数方程为:  (t为参数),
(t为参数),
∴消去参数得l的直角坐标方程为:x﹣y+2=0
(2)解:将l的参数方程:  (t为参数)代入y2=2ax,(a>0),
(t为参数)代入y2=2ax,(a>0),
得: ![]() ,
,
△=8a2﹣32a>0,解得a>4,
![]() ,t1t2=8a,
,t1t2=8a,
∵|PM|,|MN|,|PN|成等比数列,
∴|t1﹣t2|2=|t1t2|,∴(2 ![]() )2﹣4×8a=8a,
)2﹣4×8a=8a,
解得a=5
【解析】(1)曲线C转化为ρ2sin2θ=2aρcosθ,(a>0),由此能求出曲线C的普通方程;l的参数方程消去参数能求出l的直角坐标方程.(2)将l的参数方程代入曲线C的普通方程,得: ![]() ,由根的差别式得a>4,由韦达定理得
,由根的差别式得a>4,由韦达定理得 ![]() ,t1t2=8a,由此利用|PM|,|MN|,|PN|成等比数列,能求出a.
,t1t2=8a,由此利用|PM|,|MN|,|PN|成等比数列,能求出a.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=m﹣|x﹣2|,m∈R,且f(x+2)≥0的解集为[﹣3,3].
(Ⅰ)解不等式:f(x)+f(x+2)>0;
(Ⅱ)若a,b,c均为正实数,且满足a+b+c=m,求证: ![]() ≥3.
≥3.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在(0,+∞)上的函数f(x)的导函数为f'(x),满足x2f'(x)+xf(x)=lnx,f(e)= ![]() ,则f(x)( )
,则f(x)( )
A.有极大值,无极小值
B.有极小值,无极大值
C.既有极大值又有极小值
D.既无极大值也无极小值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆Γ: ![]() +
+ ![]() =1(a>b>0)的离心率与双曲线x2﹣y2=a2的离心率之和为
=1(a>b>0)的离心率与双曲线x2﹣y2=a2的离心率之和为 ![]() ,B1、B2为椭圆Γ短轴的两个端点,P是椭圆Γ上一动点(不与B1、B2重合),直线B1P、B2P分别交直线l:y=4于M、N两点,△B1B2P的面积记为S1 , △PMN的面积记为S2 , 且S1的最大值为4
,B1、B2为椭圆Γ短轴的两个端点,P是椭圆Γ上一动点(不与B1、B2重合),直线B1P、B2P分别交直线l:y=4于M、N两点,△B1B2P的面积记为S1 , △PMN的面积记为S2 , 且S1的最大值为4 ![]() .
.
(1)求椭圆Γ的方程;
(2)若S2=λS1 , 当λ取最小值时,求点P的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an},a1=﹣ll,公差d≠0,且a2 , a5 , a6成等比数列.
(1)求数列{an}的通项公式;
(2)若bn=|an|,求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC中,角A,B,C的对边分别为a,b,c,且三角形的面积S= ![]() accosB.
accosB.
(1)求角B的大小;
(2)若a=2 ![]() ,点D在AB的延长线上,且AD=3,cos∠ADC=
,点D在AB的延长线上,且AD=3,cos∠ADC= ![]() ,求b的值.
,求b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某年高考中,某省10万考生在满分为150分的数学考试中,成绩分布近似服从正态分布N(110,100),则分数位于区间(130,150]分的考生人数近似为( ) (已知若X~N(μ,σ2),则P(μ﹣σ<X<μ+σ)=0.6826,P(μ﹣2σ<X<μ+2σ)=0.9544,P(μ﹣3σ<X<μ+3σ)=0.9974.
A.1140
B.1075
C.2280
D.2150
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是定义在
是定义在![]() 上的偶函数,且当
上的偶函数,且当![]() 时,
时,![]() .现已画出函数
.现已画出函数![]() 在
在![]() 轴左侧的图象,如图所示,根据图象:
轴左侧的图象,如图所示,根据图象:

(1)请将函数![]() 的图象补充完整并写出该函数的增区间(不用证明).
的图象补充完整并写出该函数的增区间(不用证明).
(2)求函数![]() 的解析式.
的解析式.
(3)若函数![]() ,求函数
,求函数![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() (e为自然对数的底数).
(e为自然对数的底数).
(1)当a=b=0时,直接写出f(x)的值域(不要求写出求解过程);
(2)若a= ![]() ,求函数f(x)的单调区间;
,求函数f(x)的单调区间;
(3)若f(1)=1,且方程f(x)=1在(0,1)内有解,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com