
分析 (1)求出每件产品的利润,乘以价格得到利润y(万元)与每件产品的售价x的函数关系式;
(2)求出利润函数的导函数,可得函数在[9,11]上的单调性,即可得到利润函数的最值.
解答 解:(1)分公司一年的利润y(万元)与售价x的函数关系式为
L=(x-3-3)(12-x)2=(x-6)(144+x2-24x)
=x3-30x2+288x-864,x∈[9,11];
(2)函数的导数为y′=3x2-60x+288
=3(x2-20x+96)=3(x-12)(x-8),
当x∈[9,11]时,y′<0,L单调递减,
于是当每件产品的售价x=9时,
该分公司一年的利润最大,且最大利润ymax=27万元.
点评 本题考查函数、导数及其应用等知识,考查运用数学知识分析和解决实际问题的能力,是中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | (1,0) | B. | (0,1) | C. | (1,2) | D. | (0,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
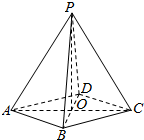 如图,在四棱锥P-ABCD中,底面ABCD是菱形,AC∩BD=O.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,AC∩BD=O.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{9}$ | D. | $\frac{1}{8}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com