练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设P0(x0，y0)为曲线C：y＝x2(x＞0)上的点，过P0作曲线C的切线与x轴交于点Q1，过Ql作平行于y轴的直线与曲线C交于点P1(xl，y1)，然后再过P1作曲线C的切线交x轴于点Q2，过Q2作平行于y轴的直线与曲线C交于点P2(x2，y2)，依此类推，作出以下各点：P0，Q1，P1，Q2，P2，Q3，…，Pn，Qn+l，…．已知x0＝2，设Pn坐标为(xn，yn)(n∈N)．

    (1)求出过点P0的切线的方程；

    (2)设xn＝f(n)，求f(n)的表达式．

    答案：
    解析：


    提示：

    本题解答运用了数形结合的思想．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    如图，设P0是抛物线y=x2上一点，且在第一象限．过点P0作抛物线的切线，交x轴于Q1点，过Q1点作x轴的垂线，交抛物线于P1点，此时就称P0确定了P1．依此类推，可由P1确定P2，…．记Pn（xn，yn），n=0，1，2，…．给出下列三个结论：
    ①xn＞0；
    ②数列{xn}为单调递减数列；
    ③对于?n∈N，?x0＞1，使得y0+y1+y2+…+yn＜2．
    其中所有正确结论的序号为
    ①②③
    ①②③
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2013•海淀区一模）设A（xA，yA），B（xB，yB）为平面直角坐标系上的两点，其中xA，yA，BxB，yB∈Z．令△x=xB-xA，△y=yB-yA，若|△x|+|△y=3，且|△x|-|△y|≠0，则称点B为点A的“相关点”，记作：B=i（A）．
    （Ⅰ）请问：点（0，0）的“相关点”有几个？判断这些点是否在同一个圆上，若在，写出圆的方程；若不在，说明理由；
    （Ⅱ）已知点H（9，3），L（5，3），若点M满足M=i（H），L=i（M），求点M的坐标；
    （Ⅲ）已知P0（x0，y0）（x0∈Z，Y0∈Z）为一个定点，点列{Pi}满足：Pi=i（Pi-1），其中i=1，2，3，…，n，求|P0Pn|的最小值．

    查看答案和解析>>

    科目：高中数学 来源：福建省厦门翔安一中2011－2012学年高二上学期期中考试数学理科试题 题型：013

    设P0(x0，y0)为圆x2＋(y－1)2＝1上的任意一点，要使不等式x0－y0－c≤0恒成立，则c的取值范围是

    [　　]
    A．

    [0，＋∞)

    B．

    [－1，＋∞)

    C．

    (－∞，＋1]

    D．

    [1－，＋∞)

    查看答案和解析>>

    科目：高中数学 来源：南通高考密卷·数学（理） 题型：044

    设C：y＝x2(x＞0)上的点为P0(x0，y0)，过P0作曲线C的切线与x轴交于Q1，过Q1作平行于y轴的直线与曲线C交于P1(x1，y1)，然后再过P1作曲线C的切线与x轴交于Q2，过Q2作平行于y轴的直线与曲线C交于P2(x2，y2)，依次类推，作出以下各点：Q3，P3，…，Pn，Qn+1，…．已知x0＝2，设Pn(xn，yn)(n∈N)．

    (1)设xn＝f(n)，求f(n)的表达式；

    (2)求g(n)＝；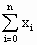

    (3)设Sn＝[g(n)－4]log2f(n)．若n＞2，求证：－1≤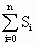＜0．

    查看答案和解析>>

    同步练习册答案