解:(1)∵

,

,
又

,
而y=sinx在

上递减,
∴
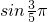
>

,即
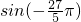
>
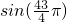
.
(2)∵tan2007°=tan207°,tan2008°=tan208°,
又180°<207°<208°<270°,
而y=tanx在(180°,270°)上递增,
∴tan207°<tan208°,即tan2007°<tan2008°.
分析:(1)先利用诱导公式化简,
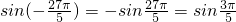
,sin

,利用正弦函数y=sinx在区间

上的单调性判断.
(2)利用诱导公式化简可得,tan2007°=tan(1800
0+207
0)=tan207°,tan2008°=tan208°,结合正切函数y=tanx在(180
0,270
0)上的单调性可判断tan207°与tan208°的大小,从而判断原式的大小.
点评:本题主要考查了正弦函数y=sinx,y=tanx在相应区间上的单调性的应用,利用单调性判断函数值的大小的前提是先用诱导公式把函数式化简到同一个单调区间,然后利用函数在单调区间上的单调性进行判断.

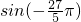 和
和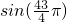 ;
; ,
, ,
, ,
, 上递减,
上递减,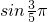 >
> ,即
,即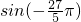 >
>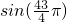 .
.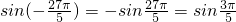 ,sin
,sin ,利用正弦函数y=sinx在区间
,利用正弦函数y=sinx在区间 上的单调性判断.
上的单调性判断.

 名校课堂系列答案
名校课堂系列答案