
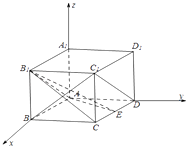
【题目】如图,在长方体ABCD﹣A1B1C1D1中,AA1=AD=1,E为CD中点. 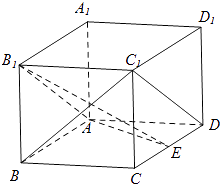
(1)求证:C1D∥平面AB1E;
(2)求证:BC1⊥B1E;
(3)若AB= ![]() ,求二面角E﹣AB1﹣B的正切值.
,求二面角E﹣AB1﹣B的正切值.
【答案】
(1)证明:由长方体性质可知,B1C1∥BC,BC∥AD,且三者都相等
∴四边形B1C1DA是平行四边形,C1D∥D1A
∵C1D平面AB1E,AB1平面AB1E,
∴C1D∥平面AB1E.
(2)证明:连结B1C,由长方体性质可知,CD⊥平面BC1BC1平面BC1,
∴CD⊥BC1,又AA1=AD,
∴四边形BCC1B1是正方形,BC1⊥B1C,
又B1C∩CD=D,∴BC1⊥平面B1CEB1E平面B1CE,∴BC1⊥B1E.
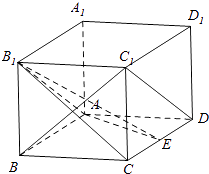
(3)解:
法一:设F是线段AB中点,连结EF
∵EF∥AD,AD⊥平面AA1B1B,
∴EF⊥平面AA1B1B,EF⊥AB1,作FG⊥AB1,EF∩FG=F,
∴AB1⊥平面EFG,AB1⊥EG,∠EGF是二面角E﹣AB1﹣B的平面角,)
直角三角形FGA中,
![]() ,
, ![]() ,
, ![]() .
.
直角三角形EFG中, ![]()
∴二面角E﹣AB1﹣B的正切值 ![]()
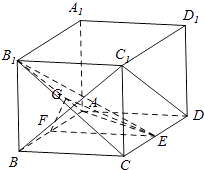
法二:以A为原点,AB,AD,AA1分别为x,y,z轴建立空间坐标系.
则A(0,0,0), ![]() ,
, ![]() ,
, ![]()
![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
,
设平面AB1E的法向量为 ![]() ,
,
由 ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
得: ![]() ,令y=1,得
,令y=1,得 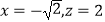 ,
, ![]() ,
,
设向量 ![]() 与
与 ![]() 的夹角为θ,则
的夹角为θ,则 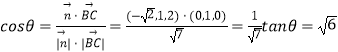 ,
,
∴二面角E﹣AB1﹣B的正切值为 ![]() .
.
【解析】(1)推导出四边形B1C1DA是平行四边形,从而C1D∥D1A,由此能证明C1D∥平面AB1E.(2)连结B1C,推导出CD⊥BC1 , 从而四边形BCC1B1是正方形,BC1⊥B1C,由此能证明BC1⊥B1E.(3)法一:设F是线段AB中点,连结EF,作FG⊥AB1 , 则∠EGF是二面角E﹣AB1﹣B的平面角,由此能求出二面角E﹣AB1﹣B的正切值.法二:以A为原点,AB,AD,AA1分别为x,y,z轴建立空间坐标系,利用向量法能求出二面角E﹣AB1﹣B的正切值.
【考点精析】通过灵活运用直线与平面平行的判定,掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行即可以解答此题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
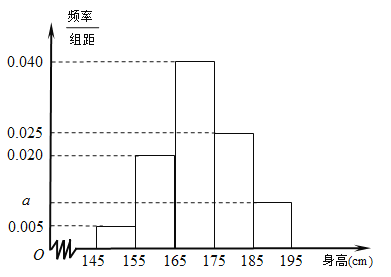
【题目】某中学随机选取了![]() 名男生,将他们的身高作为样本进行统计,得到如图所示的频率分布直方图.观察图中数据,完成下列问题.
名男生,将他们的身高作为样本进行统计,得到如图所示的频率分布直方图.观察图中数据,完成下列问题.
(Ⅰ)求![]() 的值及样本中男生身高在
的值及样本中男生身高在![]() (单位:
(单位: ![]() )的人数;
)的人数;
(Ⅱ)假设同一组中的每个数据可用该组区间的中点值代替,通过样本估计该校全体男生的平均身高;
(Ⅲ)在样本中,从身高在![]() 和
和![]() (单位:
(单位: ![]() )内的男生中任选两人,求这两人的身高都不低于
)内的男生中任选两人,求这两人的身高都不低于![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某媒体为了解某地区大学生晚上放学后使用手机上网情况,随机抽取了100名大学生进行调查.如图是根据调查结果绘制的学生每晚使用手机上网平均所用时间的频率分布直方图.将时间不低于40分钟的学生称为“手机迷”. 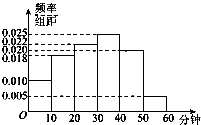
(1)样本中“手机迷”有多少人?
(2)根据已知条件完成下面的2×2列联表,并据此资料判断是否有95%的把握认为“手机迷”与性别有关?
(3)将上述调查所得到的频率视为概率.现在从该地区大量大学 生中,采用随机抽样方法每次抽取1名大学生,抽取3次,经调查一名“手机迷”比“非手机迷”每月的话费平均多40元,记被抽取的3名大学生中的“手机迷”人数为X,且设3人每月的总话费比“非手机迷”共多出Y元,若每次抽取的结果是相互独立的,求X的分布列和Y的期望EY
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设等差数列{an}的前n项和为Sn , a2=4,S5=30
(1)求数列{an}的通项公式an
(2)设数列{ ![]() }的前n项和为Tn , 求证:
}的前n项和为Tn , 求证: ![]() ≤Tn<
≤Tn< ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足an+1+an=4n﹣3,n∈N*
(1)若数列{an}是等差数列,求a1的值;
(2)当a1=﹣3时,求数列{an}的前n项和Sn;
(3)若对任意的n∈N* , 都有 ![]() ≥5成立,求a1的取值范围.
≥5成立,求a1的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某搜索引擎广告按照付费价格对搜索结果进行排名,点击一次付费价格排名越靠前,被点击的次数也可能会提高,已知某关键词被甲、乙等多个公司竞争,其中甲、乙付费情况与每小时点击量结果绘制成如下的折线图.

(1)试根据所给数据计算每小时点击次数的均值方差并分析两组数据的特征;
(2)若把乙公司设置的每次点击价格为x,每小时点击次数为![]() ,则点
,则点![]() 近似在一条直线附近.试根据前5次价格与每小时点击次数的关系,求y关于x的回归直线
近似在一条直线附近.试根据前5次价格与每小时点击次数的关系,求y关于x的回归直线![]() .(附:回归方程系数公式:
.(附:回归方程系数公式: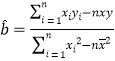 ,
,![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和Sn满足2Sn=3an﹣3,数列{bn}的前n项和Tn满足 ![]() =
= ![]() +1且b1=1.
+1且b1=1.
(1)求数列{an},{bn}的通项公式;
(2)设cn= ![]() ,求数列{cn}的前n项和Pn;
,求数列{cn}的前n项和Pn;
(3)数列{Sn}中是否存在不同的三项Sp , Sq , Sr , 使这三项恰好构成等差数列?若存在,求出p,q,r的关系;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】双曲线 ![]() =1(a>0,b>0)的左右焦点分别为F1 , F2渐近线分别为l1 , l2 , 位于第一象限的点P在l1上,若l2⊥PF1 , l2∥PF2 , 则双曲线的离心率是( )
=1(a>0,b>0)的左右焦点分别为F1 , F2渐近线分别为l1 , l2 , 位于第一象限的点P在l1上,若l2⊥PF1 , l2∥PF2 , 则双曲线的离心率是( )
A.![]()
B.![]()
C.2
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com