
【题目】2019年春节期间,我国高速公路继续执行“节假日高速公路免费政策”某路桥公司为掌握春节期间车辆出行的高峰情况,在某高速公路收费点记录了大年初三上午9:20~10:40这一时间段内通过的车辆数,统计发现这一时间段内共有600辆车通过该收费点,它们通过该收费点的时刻的频率分布直方图如下图所示,其中时间段9:20~9:40记作区间![]() ,9:40~10:00记作
,9:40~10:00记作![]() ,10:00~10:20记作
,10:00~10:20记作![]() ,10:20~10:40记作
,10:20~10:40记作![]() .例如:10点04分,记作时刻64.
.例如:10点04分,记作时刻64.
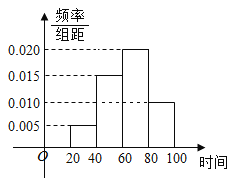
(1)估计这600辆车在9:20~10:40时间段内通过该收费点的时刻的平均值(同一组中的数据用该组区间的中点值代表);
(2)为了对数据进行分析,现采用分层抽样的方法从这600辆车中抽取10辆,再从这10辆车中随机抽取4辆,设抽到的4辆车中,在9:20~10:00之间通过的车辆数为X,求X的分布列与数学期望;
(3)由大数据分析可知,车辆在每天通过该收费点的时刻T服从正态分布![]() ,其中
,其中![]() 可用这600辆车在9:20~10:40之间通过该收费点的时刻的平均值近似代替,
可用这600辆车在9:20~10:40之间通过该收费点的时刻的平均值近似代替,![]() 可用样本的方差近似代替(同一组中的数据用该组区间的中点值代表),已知大年初五全天共有1000辆车通过该收费点,估计在9:46~10:40之间通过的车辆数(结果保留到整数).
可用样本的方差近似代替(同一组中的数据用该组区间的中点值代表),已知大年初五全天共有1000辆车通过该收费点,估计在9:46~10:40之间通过的车辆数(结果保留到整数).
参考数据:若![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
【答案】(1)10点04分(2)分布列见解析,![]() (3)819辆
(3)819辆
【解析】
(1)利用频率分布直方图和平均数的计算公式,即可求得这600辆车在9:20~10:40时间段内通过该收费点的时刻的平均值;
(2)结合频率分布直方图和分层抽样的方法求得随机变量![]() 的可能取值
的可能取值![]() ,求出相应的概率,得到
,求出相应的概率,得到![]() 的分布列,利用期望的公式,求得其数学期望;
的分布列,利用期望的公式,求得其数学期望;
(3)由(1)可得![]() ,得到
,得到![]() ,得到概率,即可求解在9:46~10:40这一时间段内通过的车辆数.
,得到概率,即可求解在9:46~10:40这一时间段内通过的车辆数.
(1)由题意,这600辆车在9:20~10:40时间段内通过该收费点的时刻的平均值为
![]() ,即10点04分.
,即10点04分.
(2)结合频率分布直方图和分层抽样的方法可知:抽取的10辆车中,在10:00前通过的车辆数就是位于时间分组中在![]() 这一区间内的车辆数,即
这一区间内的车辆数,即![]() ,所以X的可能取值为0,1,2,3,1.
,所以X的可能取值为0,1,2,3,1.
所以![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
所以X的分布列为
X | 0 | 1 | 2 | 3 | 4 |
P |
|
|
|
|
|
所以![]() .
.
(3)由(1)可得![]() ,
,
![]() ,
,
所以![]() .
.
估计在9:46~10:40这一时间段内通过的车辆数,也就是![]() 通过的车辆数,
通过的车辆数,
由![]() ,
,
![]() ,
,
所以,估计在9:46~10:40这一时间段内通过的车辆数为![]() 辆.
辆.


科目:高中数学 来源: 题型:
【题目】棱长为1的正方体![]() 内部有一圆柱
内部有一圆柱![]() ,此圆柱恰好以直线
,此圆柱恰好以直线![]() 为轴.有下列命题:
为轴.有下列命题:
①圆柱![]() 的母线与正方体
的母线与正方体![]() 所有的棱所成的角都相等;
所有的棱所成的角都相等;
②正方体![]() 所有的面与圆柱
所有的面与圆柱![]() 的底面所成的角都相等;
的底面所成的角都相等;
③在正方体![]() 内作与圆柱
内作与圆柱![]() 底面平行的截面,则截面的面积
底面平行的截面,则截面的面积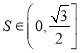 ;
;
④圆柱![]() 侧面积的最大值为
侧面积的最大值为![]() .
.
其中正确的命题是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】把方程![]() 表示的曲线作为函数
表示的曲线作为函数![]() 的图象,则下列结论正确的是( )
的图象,则下列结论正确的是( )
①![]() 在R上单调递减
在R上单调递减
②![]() 的图像关于原点对称
的图像关于原点对称
③![]() 的图象上的点到坐标原点的距离的最小值为3
的图象上的点到坐标原点的距离的最小值为3
④函数![]() 不存在零点
不存在零点
A.①③B.①②③C.①③④D.①②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知某市穿城公路![]() 自西向东到达市中心
自西向东到达市中心![]() 后转向东北方向,
后转向东北方向,![]() ,现准备修建一条直线型高架公路
,现准备修建一条直线型高架公路![]() ,在
,在![]() 上设一出入口
上设一出入口![]() ,在
,在![]() 上设一出入口
上设一出入口![]() ,且要求市中心
,且要求市中心![]() 到
到![]() 所在的直线距离为
所在的直线距离为![]() .
.
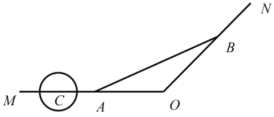
(1)求![]() ,
,![]() 两出入口间距离的最小值;
两出入口间距离的最小值;
(2)在公路![]() 段上距离市中心
段上距离市中心![]() 点
点![]() 处有一古建筑
处有一古建筑![]() (视为一点),现设立一个以
(视为一点),现设立一个以![]() 为圆心,
为圆心,![]() 为半径的圆形保护区,问如何在古建筑
为半径的圆形保护区,问如何在古建筑![]() 和市中心
和市中心![]() 之间设计出入口
之间设计出入口![]() ,才能使高架公路及其延长线不经过保护区?
,才能使高架公路及其延长线不经过保护区?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】交通安全法有规定:机动车行经人行横道时,应当减速行驶;遇行人正在通过人行横道,应当停车让行.机动车行经没有交通信号的道路时,遇行人横过马路,应当避让.我们将符合这条规定的称为“礼让斑马线”,不符合这条规定的称为“不礼让斑马线”.下表是六安市某十字路口监控设备所抓拍的5个月内驾驶员“不礼让斑马线”行为的统计数据:
月份 | 1 | 2 | 3 | 4 | 5 |
“不礼让斑马线”的驾驶员人数 | 120 | 105 | 100 | 85 | 90 |
(1)根据表中所给的5个月的数据,可用线性回归模型拟合![]() 与
与![]() 的关系,请用相关系数加以说明;
的关系,请用相关系数加以说明;
(2)求“不礼让斑马线”的驾驶员人数![]() 关于月份
关于月份![]() 之间的线性回归方程;
之间的线性回归方程;
(3)若从4,5月份“不礼让斑马线”的驾驶员中分别选取4人和2人,再从所选取的6人中任意抽取2人进行交规调查,求抽取的2人分别来自两个月份的概率;
参考公式:线性回归方程![]() ,其中
,其中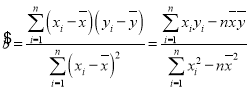 ,
,![]() ,
, .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在直角梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,点E在
,点E在![]() 上,且
上,且![]() ,将三角形
,将三角形![]() 沿线段
沿线段![]() 折起到
折起到![]() 的位置,
的位置,![]() (如图2).
(如图2).
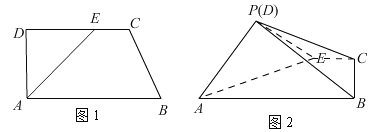
(1)求证:平面![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在点M,使
上是否存在点M,使![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=axex,g(x)=x2+2x+b,若曲线y=f(x)与曲线y=g(x)都过点P(1,c).且在点P处有相同的切线l.
(Ⅰ)求切线l的方程;
(Ⅱ)若关于x的不等式k[ef(x)]≥g(x)对任意x∈[﹣1,+∞)恒成立,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某市![]() 年全社会固定资产投资以及增长率如图所示,则下列说法错误的是( )
年全社会固定资产投资以及增长率如图所示,则下列说法错误的是( )
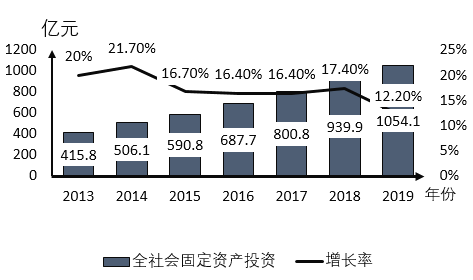
A.从2013年到2019年全社会固定资产的投资处于不断增长的状态
B.从2013年到2019年全社会固定资产投资的平均值为![]() 亿元
亿元
C.该市全社会固定资产投资增长率最高的年份为2014年
D.2016年到2017年全社会固定资产的增长率为0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com