
【题目】已知函数![]() ,
, ![]() .
.
(Ⅰ)讨论函数![]() 的单调区间;
的单调区间;
(Ⅱ)若函数![]() 在
在![]() 处取得极值,对
处取得极值,对![]() ,
, ![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1) 当![]() 时,
时, ![]() 的单调递减区间是
的单调递减区间是![]() ,无单调递增区间;当
,无单调递增区间;当![]() 时,
时, ![]() 的单调递减区间是
的单调递减区间是![]() ,单调递增区间是
,单调递增区间是![]() (2)
(2) ![]()
【解析】试题分析:(1)![]() 对a分类讨论确定函数
对a分类讨论确定函数![]() 的单调区间;(2)由函数
的单调区间;(2)由函数![]() 在
在![]() 处取得极值,确定
处取得极值,确定![]() ,对
,对![]() ,
, ![]() 恒成立即
恒成立即![]() 对
对![]() 恒成立,构造新函数求最值即可.
恒成立,构造新函数求最值即可.
试题解析:
(1)①在区间![]() 上,
上, ![]() ,
,
当![]() 时,
时, ![]() 恒成立,
恒成立, ![]() 在区间
在区间![]() 上单调递减;
上单调递减;
当![]() 时,令
时,令![]() 得
得![]() ,在区间
,在区间![]() 上,
上,
![]() ,函数
,函数![]() 单调递减,在区间
单调递减,在区间![]() 上,
上,
![]() ,函数
,函数![]() 单调递增.
单调递增.
综上所述:当![]() 时,
时, ![]() 的单调递减区间是
的单调递减区间是![]() ,无单调递增区间;
,无单调递增区间;
当![]() 时,
时, ![]() 的单调递减区间是
的单调递减区间是![]() ,单调递增区间是
,单调递增区间是![]()
②因为函数![]() 在
在![]() 处取得极值,
处取得极值,
所以![]() ,解得
,解得![]() ,经检验可知满足题意.
,经检验可知满足题意.
由已知![]() ,即
,即![]() ,
,
即![]() 对
对![]() 恒成立,
恒成立,
令![]() ,
,
则![]() ,
,
易得![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
所以![]() ,即
,即![]() .
.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱![]() 中,
中, ![]() ,
, ![]() ,点
,点![]() 为
为![]() 的中点,点
的中点,点![]() 为
为![]() 上一动点.
上一动点.

(1)是否存在一点![]() ,使得线段
,使得线段![]() 平面
平面![]() ?若存在,指出点
?若存在,指出点![]() 的位置,若不存在,请说明理由.
的位置,若不存在,请说明理由.
(2)若点![]() 为
为![]() 的中点且
的中点且![]() ,求二面角
,求二面角![]() 的正弦值.
的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了全面贯彻党的教育方针,坚持以人文本、德育为先,全面推进素质教育,让学生接触自然,了解社会,拓宽视野,丰富知识,提高社会实践能力和综合素质,减轻学生过重负担,培养学生兴趣爱好,丰富学生的课余生活,使广大学生在社会实践中,提高创新精神和实践能力,树立学生社会责任感,因此学校鼓励学生利用课余时间参加社会活动实践。寒假归来,某校高三(2)班班主任收集了所有学生参加社会活动信息,整理出如图所示的图。

(1)求高三(2)班同学人均参加社会活动的次数;
(2)求班上的小明同学仅参加1次社会活动的概率;
(3)用分层抽样的方法从班上参加活动2次及以上
的同学中抽取一个容量为5的样本,从这5人中任选3人,其中仅有两人参加2次活动的概率。.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱柱![]() 中,三个侧面均为矩形,底面
中,三个侧面均为矩形,底面![]() 为等腰直角三角形,
为等腰直角三角形, ![]() ,点
,点![]() 为棱
为棱![]() 的中点,点
的中点,点![]() 在棱
在棱![]() 上运动.
上运动.
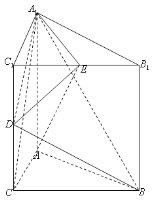
(1)求证![]()
![]()
![]() ;
;
(2)当点![]() 运动到某一位置时,恰好使二面角
运动到某一位置时,恰好使二面角![]() 的平面角的余弦值为
的平面角的余弦值为![]() ,求点
,求点![]() 到平面
到平面![]() 的距离;
的距离;
(3)在(2)的条件下,试确定线段![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,确定其位置;若不存在,说明理由.
?若存在,确定其位置;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABCA1B1C1中,BC=BB1,∠BAC=∠BCA=![]() ∠ABC,点E是A1B与AB1的交点,点D在线段AC上,B1C∥平面A1BD.
∠ABC,点E是A1B与AB1的交点,点D在线段AC上,B1C∥平面A1BD.
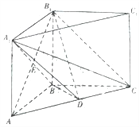
(1)求证:BD⊥A1C;
(2)求证:AB1⊥平面A1BC。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C的两个焦点分别为F1(-1,0)、F2(1,0),短轴的两个端点分别为B1,B2
(1)若△F1B1B2为等边三角形,求椭圆C的方程;
(2)若椭圆C的短轴长为2,过点F2的直线l与椭圆C相交于P,Q两点,且![]() ,求直线l的方程.
,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(Ⅰ)求函数![]() 的单调区间;
的单调区间;
(Ⅱ)试探究函数![]() 在定义域内是否存在零点,若存在,请指出有几个零点;若不存在,请说明理由;
在定义域内是否存在零点,若存在,请指出有几个零点;若不存在,请说明理由;
(Ⅲ)若![]() ,且
,且![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】牡丹江一中2019年将实行新课程改革,即除语、数、外三科为必考科目外,还要在理、化、生、史、地、政六科中选择三科作为选考科目.已知某生的高考志愿为北京大学环境科学专业,按照17年北大高考招生选考科目要求物、化必选,为该生安排课表(上午四节、下午四节,上午第四节和下午第一节不算相邻),现该生某天最后两节为自习课,且数学不排下午第一节,语文、外语不相邻,则该生该天课表有( )种.
A. 444B. 1776C. 1440D. 1560
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com