
【题目】已知函数![]() .
.
(1)若![]() ,求函数
,求函数![]() 的单调递增区间;
的单调递增区间;
(2)当![]() 时,若对任意的
时,若对任意的![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】某服装厂生产一种服装,每件服装的成本为40元,出厂单价为60元,该厂为鼓励销售商订购,决定当一次订购量超过100件时,每多订购一件,订购的全部服装的出厂单价就降低0.02元,根据市场调查,销售商一次订购量不会超过500件.
(1)设一次订购量为x件,服装的实际出厂单价为P元,写出函数![]() 的表达式;
的表达式;
(2)当销售商一次订购450件服装时,该服装厂获得的利润是多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】几位大学生响应国家的创业号召,开发了一款应用软件.为激发大家学习数学的兴趣,他们推出了“解数学题获取软件激活码”的活动.这款软件的激活码为下面数学问题的答案.如图是一个数表,第1行依次写着从小到大的正整数,然后把每行相邻的两个数的和写在这两数正中间的下方,得到下一行,数表从上到下与从左到右均为无限项,求满足如下条件的最小四位整数![]() :第2017行的第
:第2017行的第![]() 项为2的正整数幂.已知
项为2的正整数幂.已知![]() ,那么该款软件的激活码是( )
,那么该款软件的激活码是( )

A. 1040 B. 1045 C. 1060 D. 1065
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3-3x及y=f(x)上一点P(1,-2),过点P作直线l.
(1)求使直线l和y=f(x)相切且以P为切点的直线方程;
(2)求使直线l和y=f(x)相切且切点异于点P的直线方程y=g(x).
查看答案和解析>>
科目:高中数学 来源: 题型:
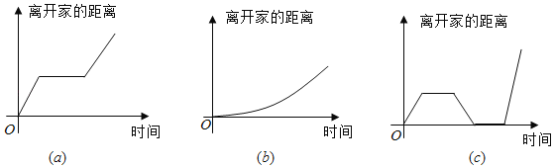
【题目】下述三个事件按顺序分别对应三个图象,正确的顺序是( )
(1)我离开家不久,发现自己把作业本忘在家里了,于是返回家里找到了作业本再上学;(2)我骑着车一路匀速行驶,只是在途中遇到一次交通堵塞,耽搁了一些时间;(3)我出发后,心情轻松,缓慢行进,后来为了赶时间开始加速.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)讨论函数f(x)=![]() ex的单调性,并证明当x>0时,(x-2)ex+x+2>0.
ex的单调性,并证明当x>0时,(x-2)ex+x+2>0.
(2)证明:当a∈[0,1) 时,函数g(x)=![]() (x>0) 有最小值.设g(x)的最小值为h(a),求函数h(a)的值域.
(x>0) 有最小值.设g(x)的最小值为h(a),求函数h(a)的值域.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com