
分析 本题是几何概型问题,设棱长为3,∠MAA′<30°表示以A1为圆心,$\sqrt{3}$为半径的$\frac{1}{4}$圆面,其面积为$\frac{3π}{4}$,求出正方形A′B′C′D′的面积为9,即可求出∠MAA'<30°的概率.
解答 解:设棱长为3,则∠MAA′=30°时,MA′=$\sqrt{3}$,
∴∠MAA′<30°表示以A′为圆心,$\sqrt{3}$为半径的$\frac{1}{4}$圆面,其面积为$\frac{3π}{4}$,如图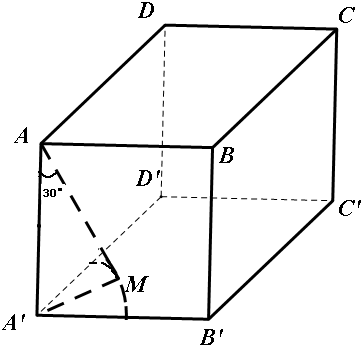 ,
,
∵正方形A′B′C′D′的面积为9,
∴∠MAA′<30°的概率P=$\frac{\frac{3π}{4}}{9}=\frac{π}{12}$;
故答案为:$\frac{π}{12}$.
点评 本小题主要考查几何概型、几何概型的应用、几何体和体积等基础知识,考查空间想象能力、化归与转化思想.属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?常数T>0,使f(x+T)=f(x) | |
| B. | ?A,图象上不存在关于原点中心对称的点 | |
| C. | ?A,f(x)存在最大值与最小值 | |
| D. | ?A,使f(x)在[a,b]上的值域也是[a,b] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com