
【题目】已知函数f(x)=![]() ,下列结论中错误的是
,下列结论中错误的是
A. ![]()
![]() , f(
, f(![]() )=0
)=0
B. 函数y=f(x)的图像是中心对称图形
C. 若![]() 是f(x)的极小值点,则f(x)在区间(-∞,
是f(x)的极小值点,则f(x)在区间(-∞,![]() )单调递减
)单调递减
D. 若![]() 是f(x)的极值点,则
是f(x)的极值点,则![]() (
(![]() )=0
)=0
【答案】C
【解析】
试题分析:由于三次函数的三次项系数为正值,当x→-∞时,函数值→-∞,当x→+∞时,函数值也→+∞,又三次函数的图象是连续不断的,故一定穿过x轴,即一定x0∈R,f(x0)=0,选项A中的结论正确;函数f(x)的解析式可以通过配方的方法化为形如(x+m)3+n(x+m)+h的形式,通过平移函数图象,函数的解析式可以化为y=x3+nx的形式,这是一个奇函数,其图象关于坐标原点对称,故函数f(x)的图象是中心对称图形,选项B中的结论正确;由于三次函数的三次项系数为正值,故函数如果存在极值点x1,x2,则极小值点x2>x1,即函数在-∞到极小值点的区间上是先递增后递减的,所以选项C中的结论错误;根据导数与极值的关系,显然选项D中的结论正确.


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:
【题目】已知存在常数![]() ,那么函数
,那么函数![]() 在
在![]() 上是减函数,在
上是减函数,在![]() 上是增函数,再由函数的奇偶性可知在
上是增函数,再由函数的奇偶性可知在![]() 上是增函数,在
上是增函数,在![]() 上是减函数.
上是减函数.
(1)判断函数![]() 的单调性,并证明:
的单调性,并证明:
(2)将前述的函数![]() 和
和![]() 推广为更为一般形式的函数
推广为更为一般形式的函数![]() ,使
,使![]() 和
和![]() 都是
都是![]() 的特例,研究
的特例,研究![]() 的单调性(只须归纳出结论,不必推理证明)
的单调性(只须归纳出结论,不必推理证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中错误的是( )
A. 给定两个命题![]() ,若
,若![]() 为真命题,则
为真命题,则![]() 都是假命题;
都是假命题;
B. 命题“若![]() ,则
,则![]() ”的逆否命题是“若
”的逆否命题是“若![]() ,则
,则![]() ”;
”;
C. 若命题![]() ,则
,则![]() ,使得
,使得![]() ;
;
D. 函数![]() 在
在![]() 处的导数存在,若
处的导数存在,若![]() 是
是![]() 的极值点,则
的极值点,则![]() 是
是![]() 的充要条件.
的充要条件.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥P﹣ABCD中,AB∥CD,AB⊥AD,AB=AD=AP=2CD=2,M是棱PB上一点.
(Ⅰ)若BM=2MP,求证:PD∥平面MAC;
(Ⅱ)若平面PAB⊥平面ABCD,平面PAD⊥平面ABCD,求证:PA⊥平面ABCD;
(Ⅲ)在(Ⅱ)的条件下,若二面角B﹣AC﹣M的余弦值为 ![]() ,求
,求 ![]() 的值.
的值.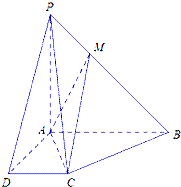
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=sin( ![]() x﹣
x﹣ ![]() )﹣2cos2
)﹣2cos2 ![]() x+1.
x+1.
(1)求f(x)的最小正周期;
(2)若函数y=f(x)与y=g(x)的图象关于直线x=1对称,求当x∈[0, ![]() ]时,y=g(x)的最大值.
]时,y=g(x)的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的公差d≠0,且a1 , a3 , a13成等比数列,若a1=1,Sn是数列{an}前n项的和,则 ![]() (n∈N+)的最小值为( )
(n∈N+)的最小值为( )
A.4
B.3
C.2 ![]() ﹣2
﹣2
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某理科考生参加自主招生面试,从7道题中(4道理科题3道文科题)不放回地依次任取3道作答.
(1)求该考生在第一次抽到理科题的条件下,第二次和第三次均抽到文科题的概率;
(2)规定理科考生需作答两道理科题和一道文科题,该考生答对理科题的概率均为![]() ,答对文科题的概率均为
,答对文科题的概率均为![]() ,若每题答对得10分,否则得零分.现该生已抽到三道题(两理一文),求其所得总分
,若每题答对得10分,否则得零分.现该生已抽到三道题(两理一文),求其所得总分![]() 的分布列与数学期望
的分布列与数学期望![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com