
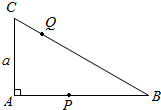
 如图,在Rt△ABC中,∠B=30°,∠C=60°,AC=a,动点P,Q自A出发分别沿边界按ABCA的方向及ACBA的方向运动,它们的速度之比是1:3,当P,Q相遇时,停止运动,点P所走过的路程为x,△APQ的面积为y,写出y关于x的函数关系式,并求出定义域.
如图,在Rt△ABC中,∠B=30°,∠C=60°,AC=a,动点P,Q自A出发分别沿边界按ABCA的方向及ACBA的方向运动,它们的速度之比是1:3,当P,Q相遇时,停止运动,点P所走过的路程为x,△APQ的面积为y,写出y关于x的函数关系式,并求出定义域. 分析 分布讨论当点P,Q在AB上,BC上,AC上,对应三角形的底的长度,和三角形的高,结合三角形的面积公式进行求解即可.
解答 解:∵在Rt△ABC中,∠B=30°,∠C=60°,AC=a,
∴AB=$\sqrt{3}$a,BC=2a,三角形的周长,为3a+$\sqrt{3}$a,
∵P,Q的速度之比是1:3,
∴P,Q的路程之比是1:3,
若点P所走过的路程为x,则点Q所走过的路程为3x,
若当P,Q相遇时,停止运动,
则3x+x=3a+$\sqrt{3}$a,
即x=$\frac{1}{4}$(3a+$\sqrt{3}$a),即x的取值范围是[0,$\frac{1}{4}$(3a+$\sqrt{3}$a)].
①当点Q在线段AC上时,0<x≤$\frac{1}{3}$a时,三角形APQ为直角三角形,S=$\frac{1}{2}x•3x=\frac{3}{2}{x}^{2}$;
②当点Q在线段CB上时,$\frac{1}{3}$a<x≤a时,作出示意图如下:
此时BQ=AC+BC-3x=3a-3x,
则△APQ的高为BQsinB=$\frac{3a-3x}{2}$,
所以S=$\frac{1}{2}$x•$\frac{3a-3x}{2}$=$\frac{3ax-3{x}^{2}}{4}$;
③当Q在线段AB上时,不能构成三角形,
所以函数f(x)=$\left\{\begin{array}{l}{\frac{3{x}^{2}}{2},}&{0<x≤\frac{1}{3}a}\\{\frac{3ax-3{x}^{2}}{4},}&{\frac{1}{3}a<x≤a}\end{array}\right.$.
点评 本题主要考查函数解析式的求解,结合三角形的面积公式是解决本题的关键.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com