
【题目】集合A是由满足以下性质的函数f(x)组成的:对于任意x≥0,f(x) ∈[-2,4]且f(x)在[0,+∞)上是增函数.
(Ⅰ)试判断![]() 与
与![]() (x≥0)是否属于集合A,并说明理由;
(x≥0)是否属于集合A,并说明理由;
(Ⅱ)对于(Ⅰ)中你认为属于集合A的函数f(x),证明:对于任意的x≥0,都有f(x)+f(x+2)<2f(x+1).
【答案】(1) ![]() ,
, ![]() (2)见解析.
(2)见解析.
【解析】试题分析:(I)由已知可得函数![]() 的值域
的值域![]() ,从而可得
,从而可得![]() ,对于
,对于![]() ,只要分别判断函数定义域是否满足条件①,值域是否满足条件②,单调性是否满足条件③,即可得答案;(II)由(I)知,
,只要分别判断函数定义域是否满足条件①,值域是否满足条件②,单调性是否满足条件③,即可得答案;(II)由(I)知, ![]() 属于集合
属于集合![]() ,原不等式为
,原不等式为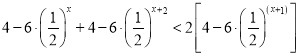 ,利用作差法指数幂的运算法则化简整理可以证明结论.
,利用作差法指数幂的运算法则化简整理可以证明结论.
试题解析:(Ⅰ) ![]() ,
, ![]() ,理由如下:
,理由如下:
由于![]() (49)=5>4,
(49)=5>4, ![]() (49)
(49)![]() [-2,4],所以
[-2,4],所以![]() (x)
(x)![]() A.
A.
对于![]()
因为![]() 在[0,+∞)上是减函数,且其值域为(0,1],
在[0,+∞)上是减函数,且其值域为(0,1],
所以![]() 在区间[0,+∞)上是增函数.
在区间[0,+∞)上是增函数.
所以![]() ≥f(0)=-2,且
≥f(0)=-2,且![]() =
=![]() <4,
<4,
所以对于任意x≥0,f(x)∈[-2,4].
所以![]() ∈A
∈A
(Ⅱ)由(Ⅰ)得: ![]() ,
,
f(x+1)=4-![]() =4-3·
=4-3·![]() ,
,
所以2f(x+1)-[f(x)+f(x+2)]=2[4-3·![]() ]-[4-6·
]-[4-6·![]() +4-
+4-![]() ·
·![]() ]=
]=![]() ·
·![]() >0,
>0,
所以对于任意的x≥0,都有f(x)+f(x+2)<2f(x+1).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知直线l:x+2y-2=0,试求:
(1)点P(-2,-1)关于直线l的对称点坐标;
(2)直线![]() 关于直线l对称的直线l2的方程;
关于直线l对称的直线l2的方程;
(3)直线l关于点(1,1)对称的直线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】端午节小长假期间,张洋与几位同学从天津乘火车到大连去旅游,若当天从天津到大连的三列火车正点到达的概率分别为0.8,0.7,0.9,假设这三列火车之间是否正点到达互不影响,则这三列火车恰好有两列正点到达的概率是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣1|﹣|x+1|.
(1)求不等式|f(x)|<1的解集;
(2)若不等式|a|f(x)≥|f(a)|对任意a∈R恒成立,求实数x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·湖南)如下图,直三棱柱ABC-A1B1C1的底面是边长为2的正三角形,E、F分别是BC、CC1的中点.
(1)证明:平面AEF⊥平面B1BCC1;
(2)若直线A1C与平面A1ABB1所成的角为45°,求三棱锥F-AEC的体积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com