
【题目】已知椭圆C1: ![]() +
+ ![]() =1(b>0)的左、右焦点分别为F1、F2 , 点F2也为抛物线C2:y2=8x的焦点,过点F2的直线l交抛物线C2于A,B两点.
=1(b>0)的左、右焦点分别为F1、F2 , 点F2也为抛物线C2:y2=8x的焦点,过点F2的直线l交抛物线C2于A,B两点.
(Ⅰ)若点P(8,0)满足|PA|=|PB|,求直线l的方程;
(Ⅱ)T为直线x=﹣3上任意一点,过点F1作TF1的垂线交椭圆C1于M,N两点,求 ![]() 的最小值.
的最小值.
【答案】解:(Ⅰ)由抛物线 ![]() 得F2(2,0),
得F2(2,0),
当直线l斜率不存在,即l:x=2时,满足题意.
当直线l斜率存在,设l:y=k(x﹣2)(k≠0),A(x1,y1),B(x2,y2),
由  得k2x2﹣(4k2+8)x+4k2=0,
得k2x2﹣(4k2+8)x+4k2=0,
∴ ![]() .
.
设AB的中点为G,则 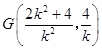 ,
,
∵|PA|=|PB|,∴PG⊥l,kPGk=﹣1,
∴  ,解得
,解得 ![]() ,则
,则 ![]() ,
,
∴直线l的方程为 ![]() 或x=2.
或x=2.
(Ⅱ)∵F2(2,0),∴ ![]() ,
,
设T点的坐标为(﹣3,m),
则直线TF1的斜率 ![]() ,
,
当m≠0时,直线MN的斜率 ![]() ,直线MN的方程是x=my﹣2,
,直线MN的方程是x=my﹣2,
当m=0时,直线MN的方程是x=﹣2,也符合x=my﹣2的形式.
∴直线MN的方程是x=my﹣2.
设M(x3,y3),N(x4,y4),则  ,得(m2+3)y2﹣4my﹣2=0,
,得(m2+3)y2﹣4my﹣2=0,
∴ ![]() ,
,
![]() ,
, ![]() =
= ![]() ,
,
∴  ,
,
当且仅当 ![]() ,即m=±1时,等号成立,此时
,即m=±1时,等号成立,此时 ![]() 取得最小值
取得最小值 ![]() .
.
【解析】(Ⅰ)由抛物线 ![]() 得F2(2,0),当直线l斜率不存在,即l:x=2时,满足题意.当直线l斜率存在,设l:y=k(x﹣2)(k≠0),A(x1,y1),B(x2,y2),与抛物线方程联立可得k2x2﹣(4k2+8)x+4k2=0,利用根与系数的关系、中点坐标公式可得AB的中点
得F2(2,0),当直线l斜率不存在,即l:x=2时,满足题意.当直线l斜率存在,设l:y=k(x﹣2)(k≠0),A(x1,y1),B(x2,y2),与抛物线方程联立可得k2x2﹣(4k2+8)x+4k2=0,利用根与系数的关系、中点坐标公式可得AB的中点 ![]() ,由|PA|=|PB|,可得PG⊥l,kPGk=﹣1,解得k即可得出.(Ⅱ)F2(2,0),可得椭圆C1的方程,设T点的坐标为(﹣3,m),则直线TF1的斜率
,由|PA|=|PB|,可得PG⊥l,kPGk=﹣1,解得k即可得出.(Ⅱ)F2(2,0),可得椭圆C1的方程,设T点的坐标为(﹣3,m),则直线TF1的斜率 ![]() =﹣m.当m≠0时,直线MN的斜率
=﹣m.当m≠0时,直线MN的斜率 ![]() ,直线MN的方程是x=my﹣2,
,直线MN的方程是x=my﹣2,
当m=0时,上述方程.设M(x3,y3),N(x4,y4),与椭圆的方程联立,利用根与系数的关系、两点之间的距离公式及其基本不等式的性质即可得出.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=mln(x+1)﹣nx在点(1,f(1))处的切线与y轴垂直,且 ![]() ,其中 m,n∈R.
,其中 m,n∈R.
(Ⅰ)求m,n的值,并求出f(x)的单调区间;
(Ⅱ)设g(x)=﹣x2+2x,确定非负实数a的取值范围,使不等式f(x)+x≥ag(x)在[0,+∞)上恒成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某网络营销部门为了统计某市网友2015年11月11日在某网店的网购情况,随机抽查了该市100名网友的网购金额情况,得到如图频率分布直方图. 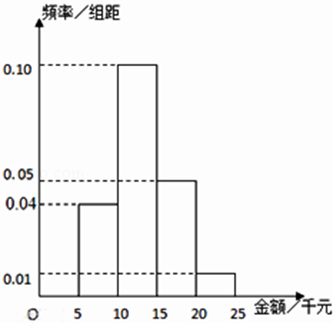
(1)估计直方图中网购金额的中位数;
(2)若规定网购金额超过15千元的顾客定义为“网购达人”,网购金额不超过15千元的顾客定义为“非网购达人”;若以该网店的频率估计全市“非网购达人”和“网购达人”的概率,从全市任意选取3人,则3人中“非网购达人”与“网购达人”的人数之差的绝对值为X,求X的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l在直角坐标系xOy中的参数方程为 ![]() 为参数,θ为倾斜角),以坐标原点O为极点,x轴正半轴为极轴,建立极坐标系,在极坐标系中,曲线的方程为ρ﹣ρcos2θ﹣4cosθ=0.
为参数,θ为倾斜角),以坐标原点O为极点,x轴正半轴为极轴,建立极坐标系,在极坐标系中,曲线的方程为ρ﹣ρcos2θ﹣4cosθ=0.
(1)写出曲线C的直角坐标方程;
(2)点Q(a,0),若直线l与曲线C交于A、B两点,求使 ![]() 为定值的值.
为定值的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy 中,F,A,B 分别为椭圆 ![]() 的右焦点、右顶点和上顶点,若
的右焦点、右顶点和上顶点,若 ![]()
(1)求a的值;
(2)过点P(0,2)作直线l 交椭圆于M,N 两点,过M 作平行于x 轴的直线交椭圆于另外一点Q,连接NQ ,求证:直线NQ 经过一个定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】规定:点P(x,y)按向量 ![]() 平移后的点为Q(x+a,y+b).若函数
平移后的点为Q(x+a,y+b).若函数 ![]() 的图象按向量
的图象按向量 ![]() =(j,k)且|j|
=(j,k)且|j| ![]() 平移后的图象对应的函数是
平移后的图象对应的函数是 ![]() +1.
+1.
(1)试求向量 ![]() 的坐标;
的坐标;
(2)在△ABC中,角A,B,C所对的边分别为a,b,c,已知f(2A)+2cos(B+C)=1, ①求角A的大小;
②若a=6,求b+c的取值范围.
另外:最后一小题也可用“余弦定理结合基本不等式”求解.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com