
科目:高中数学 来源:2015-2016学年江西省南昌市高一下学期期末考试数学试卷(解析版) 题型:选择题
省农科站要检测某品牌种子的发芽率,计划采用随机数表法从该品牌800粒种子中抽取60粒进行检测,现将这800粒种子编号如下001,002,…,800,若从随机数表第8行第7列的数7开始向右读,则所抽取的第4粒种子的编号是( ).(下表是随机数表第7行至第9行)

A.105 B.507 C.071 D.717
查看答案和解析>>
科目:高中数学 来源:2015-2016学年吉林省高一下学期期末联考数学试卷(解析版) 题型:选择题
如图, ABCD-A1B1C1D1为正方体,下面结论错误的是( ).
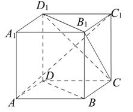
A.BD∥平面CB1D1
B.AC1⊥BD
C.AC1⊥平面CB1D1
D.异面直线AD与CB1角为60°
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
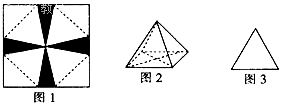 将一张边长为6cm的纸片按如图l所示阴影部分裁去四个全等的等腰三角形,将余下部分沿虚线折叠并拼成一个有底的正四棱锥(底面是正方形,顶点在底面的射影为正方形的中心)模型,如图2放置.若正四棱锥的正视图是正三角形(如图3),则正四棱锥的体积是$\frac{8\sqrt{6}}{3}$.
将一张边长为6cm的纸片按如图l所示阴影部分裁去四个全等的等腰三角形,将余下部分沿虚线折叠并拼成一个有底的正四棱锥(底面是正方形,顶点在底面的射影为正方形的中心)模型,如图2放置.若正四棱锥的正视图是正三角形(如图3),则正四棱锥的体积是$\frac{8\sqrt{6}}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com