
【题目】已知函数f(x)= 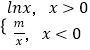 ,若f(x)﹣f(﹣x)=0有四个不同的根,则m的取值范围是( )
,若f(x)﹣f(﹣x)=0有四个不同的根,则m的取值范围是( )
A.(0,2e)
B.(0,e)
C.(0,1)
D.(0, ![]() )
)
科目:高中数学 来源: 题型:
【题目】如图1,在Rt△ABC中,∠C=90°,AC=4,BC=2,D,E分别为边AC,AB的中点,点F,G分别为线段CD,BE的中点.将△ADE沿DE折起到△A1DE的位置,使∠A1DC=60°.点Q为线段A1B上的一点,如图2. 
(Ⅰ)求证:A1F⊥BE;
(Ⅱ)线段A1B上是否存在点Q使得FQ∥平面A1DE?若存在,求出A1Q的长,若不存在,请说明理由;
(Ⅲ)当 ![]() 时,求直线GQ与平面A1DE所成角的大小.
时,求直线GQ与平面A1DE所成角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=|x﹣a|+|2x+2|﹣5(a∈R). (Ⅰ)试比较f(﹣1)与f(a)的大小;
(Ⅱ)当a≥﹣1时,若函数f(x)的图象和x轴围成一个三角形,则实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂生产不同规格的一种产品,根据检测标准,其合格产品的质量y(g)与尺寸x(mm)之间近似满足关系式y=axb(a,b为大于0的常数).现随机抽取6件合格产品,测得数据如下:
尺寸(mm) | 38 | 48 | 58 | 68 | 78 | 88 |
质量(g) | 16.8 | 18.8 | 20.7 | 22.4 | 24.0 | 25.5 |
对数据作了初步处理,相关统计量的值如下表:
|
|
|
|
75.3 | 24.6 | 18.3 | 101.4 |
(Ⅰ)根据所给数据,求y关于x的回归方程;
(Ⅱ)按照某项指标测定,当产品质量与尺寸的比在区间( ![]() ,
, ![]() )内时为优等品.现从抽取的6件合格产品中再任选3件,记ξ为取到优等品的件数,试求随机变量ξ的分布列和期望.
)内时为优等品.现从抽取的6件合格产品中再任选3件,记ξ为取到优等品的件数,试求随机变量ξ的分布列和期望.
附:对于一组数据(v1 , u1),(v2 , u2),…,(vn , un),其回归直线u=α+βv的斜率和截距的最小二乘估计分别为 ![]() =
=  ,
, ![]() =
= ![]() ﹣
﹣ ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C:y2=4x,M:(x﹣1)2+y2=4(x≥1),直线l与曲线C相交于A、B两点,O为坐标原点.
(Ⅰ)若 ![]() ,求证:直线l恒过定点,并求出定点坐标;
,求证:直线l恒过定点,并求出定点坐标;
(Ⅱ)若直线l与曲线C1相切,M(1,0),求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的内角A,B,C所对的边分别为a,b,c,且A=2C.
(1)若△ABC为锐角三角形,求 ![]() 的取值范围;
的取值范围;
(2)若b=1,c=3,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C的极坐标方程是ρ=2cosθ,以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线l的参数方程是 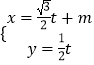 (t为参数).
(t为参数).
(1)求曲线C的直角坐标方程和直线l的普通方程;
(2)设点P(m,0),若直线l与曲线C交于A,B两点,且|PA||PB|=1,求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设样本数据x1 , x2 , …,x2017的方差是4,若yi=2xi﹣1(i=1,2,…,2017),则y1 , y2 , …y2017的方差为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com