
【题目】某校对高一年级学生寒假参加社区服务的次数进行了统计,随机抽取了![]() 名学生作为样本,得到这
名学生作为样本,得到这![]() 名学生参加社区服务的次数,根据此数据作出了频率分布统计表和频率分布直方图如下:
名学生参加社区服务的次数,根据此数据作出了频率分布统计表和频率分布直方图如下:

(1)求表中![]() 的值和频率分布直方图中
的值和频率分布直方图中![]() 的值,并根据频率分布直方图估计该校高一学生寒假参加社区服务次数的中位数;
的值,并根据频率分布直方图估计该校高一学生寒假参加社区服务次数的中位数;
(2)如果用分层抽样的方法从样本服务次数在![]() 和
和![]() 的人中共抽取6人,再从这6人中选2人,求2人服务次数都在
的人中共抽取6人,再从这6人中选2人,求2人服务次数都在![]() 的概率.
的概率.
【答案】(1)![]() ,
,![]() ,中位数为
,中位数为![]() ;(2)
;(2)![]()
【解析】
试题分析:(1)由第一组内频数为![]() ,频率为
,频率为![]() 可求出总人数为
可求出总人数为![]() ,由此可求出第二组的频率为
,由此可求出第二组的频率为![]() ,并可求频率直方图中
,并可求频率直方图中![]() ,由频率之和为
,由频率之和为![]() 可求出
可求出![]() ,频率分布直方图求出面积的一半处求出中位数即可;(2)分分层抽样的原则先求出共抽取
,频率分布直方图求出面积的一半处求出中位数即可;(2)分分层抽样的原则先求出共抽取![]() 人时在
人时在![]() 和
和![]() 的人数,再列出所有基本事件,可求2人服务次数都在
的人数,再列出所有基本事件,可求2人服务次数都在![]() 的概率.
的概率.
试题解析:(1)因![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
![]() ,
,
![]() .
.
中位数位于区间![]() ,设中位数为
,设中位数为![]() ,
,
则![]() ,所以
,所以![]() ,所以学生参加社区服务区次数的中位数为17次.
,所以学生参加社区服务区次数的中位数为17次.
(2)由题意知样本服务次数在![]() 有20人,样本服务次数在
有20人,样本服务次数在![]() 有4人,
有4人,
如果用分层抽样的方法从样本服务次数在![]() 和
和![]() 的人中共抽取6人,则抽取的服务次数在
的人中共抽取6人,则抽取的服务次数在![]() 和
和![]() 的人数分别为:
的人数分别为:![]() 和
和![]() .
.
记服务次数在![]() 为
为![]() ,在
,在![]() 的为
的为![]() .
.
从已抽取的6人任选两人的所有可能为:
![]()
![]() 共15种,
共15种,
设“2人服务次数都在![]() ”为事件
”为事件![]() ,则事件
,则事件![]() 包括
包括
![]()
![]()
共10种,
所有![]() .
.


科目:高中数学 来源: 题型:
【题目】已知直线![]() (
(![]() ).
).
(1)证明:直线![]() 过定点;
过定点;
(2)若直线不经过第四象限,求![]() 的取值范围;
的取值范围;
(3)若直线![]() 轴负半轴于
轴负半轴于![]() ,交
,交![]() 轴正半轴于
轴正半轴于![]() ,△
,△![]() 的面积为
的面积为![]() (
(![]() 为坐标原点),求
为坐标原点),求![]() 的最小值,并求此时直线
的最小值,并求此时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学将100名高二文科生分成水平相同的甲、乙两个“平行班”,每班50人.陈老师采用A,B两种不同的教学方式分别在甲、乙两个班进行教改实验.为了了解教学效果,期末考试后,陈老师对甲、乙两个班级的学生成绩进行统计分析,画出频率分布直方图(如下图).记成绩不低于90分者为“成绩优秀”.
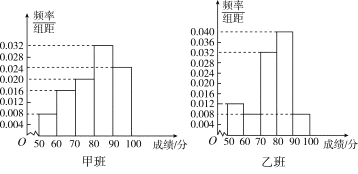
(Ⅰ)根据频率分布直方图填写下面2×2列联表;
甲班(A方式) | 乙班(B方式) | 总计 | |
成绩优秀 | |||
成绩不优秀 | |||
总计 |
(Ⅱ)判断能否在犯错误的概率不超过0.05的前提下认为:“成绩优秀”与教学方式有关?
附:![]() .
.
P(K2≥k) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
k | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】空间中任意放置的棱长为2的正四面体![]() .下列命题正确的是_________.(写出所有正确的命题的编号)
.下列命题正确的是_________.(写出所有正确的命题的编号)
①正四面体![]() 的主视图面积可能是
的主视图面积可能是![]() ;
;
②正四面体![]() 的主视图面积可能是
的主视图面积可能是![]() ;
;
③正四面体![]() 的主视图面积可能是
的主视图面积可能是![]() ;
;
④正四面体![]() 的主视图面积可能是2
的主视图面积可能是2
⑤正四面体![]() 的主视图面积可能是
的主视图面积可能是![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知以点A(-1,2)为圆心的圆与直线l1:x+2y+7=0相切.过点B(-2,0)的动直线l与圆A相交于M,N两点,Q是MN的中点,直线l与l1相交于点P.
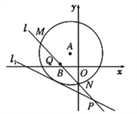
(1)求圆A的方程;
(2)当|MN|=2![]() 时,求直线l的方程.
时,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】汽车厂生产![]() 三类轿车,每类轿车均有舒适型和标准型两类型号,某月的产量如下表:(单位:辆). 按类用分层抽样的方法在这个月生产的轿车中抽取50辆,其中有
三类轿车,每类轿车均有舒适型和标准型两类型号,某月的产量如下表:(单位:辆). 按类用分层抽样的方法在这个月生产的轿车中抽取50辆,其中有![]() 类轿车10辆.
类轿车10辆.

(1)求![]() 的值;
的值;
(2)用分层抽样的方法在![]() 类轿车中抽取一个容量为5的样本,从中任取2辆,求至少有1辆舒适型轿车的概率;
类轿车中抽取一个容量为5的样本,从中任取2辆,求至少有1辆舒适型轿车的概率;
(3)用随机抽样的方法从![]() 类舒适型轿车中抽取8辆,经检测它们的得分如下:9.4,8.6,9.2,9.6,8.7,9.3,9.0,8.2,把这8辆轿车的得分看成一个总体,从中任取一个数,求该数与样本平均数之差的绝对值不超过0.5的概率.
类舒适型轿车中抽取8辆,经检测它们的得分如下:9.4,8.6,9.2,9.6,8.7,9.3,9.0,8.2,把这8辆轿车的得分看成一个总体,从中任取一个数,求该数与样本平均数之差的绝对值不超过0.5的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(Ⅰ)当![]() 时,求函数
时,求函数![]() 的极小值;
的极小值;
(Ⅱ)当![]() 时,过坐标原点
时,过坐标原点![]() 作曲线
作曲线![]() 的切线,设切点为
的切线,设切点为![]() ,求实数
,求实数![]() 的值;
的值;
(Ⅲ)设定义在![]() 上的函数
上的函数![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() :
: ![]() ,当
,当![]() 时,若
时,若![]() 在
在![]() 内恒成立,则称
内恒成立,则称![]() 为函数
为函数![]() 的“转点”.当
的“转点”.当![]() 时,试问函数
时,试问函数![]() 是否存在“转点”.若存在,请求出“转点”的横坐标,若不存在,请说明理由.
是否存在“转点”.若存在,请求出“转点”的横坐标,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com