
6个人站成一排,甲、乙二人不相邻的不同站法有多少种?
|
解法 1 排除法.将甲、乙相邻二人视为一个整体,当做一个元素,与其他 4个元素(人)站成一排,有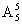 种站法.注意到甲、乙二人可交换位置,则甲、乙二人相邻共有2 种站法.注意到甲、乙二人可交换位置,则甲、乙二人相邻共有2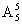 种站法.显然这些站法是不合要求的.另外,6个人站成一排共有 种站法.显然这些站法是不合要求的.另外,6个人站成一排共有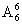 种站法,故符合条件的站法有 种站法,故符合条件的站法有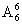 -2 -2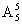 =480种. =480种.
解法 2 插入法.先让甲、乙以外的 4个人站成一排,有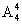 种站法.这4个人之间连同两端共有5个空档,将甲、乙二人站在其中的2个空档里,有 种站法.这4个人之间连同两端共有5个空档,将甲、乙二人站在其中的2个空档里,有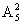 种站法.故符合条件的不同站法有 种站法.故符合条件的不同站法有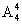 · ·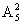 =24×20=480种. =24×20=480种.
注意,站队问题中常有“某些元素不相邻”的限制条件,解决此类问题一般有两种方法.例如解法 1将问题转化为求这些元素相邻问题,再用原题中的排列总数减去这些元素相邻的排列数,所得差即为所求,这就是常用的排除法;又如解法2,可将没有限制的不相邻的元素先排列,考虑它们之间及两端的空档,然后再把不允许相邻的元素选空插进去,这就是常用的插入法. |


科目:高中数学 来源:2011-2012学年重庆49中高三(下)第一次质量抽测数学试卷(理科)(解析版) 题型:选择题
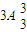

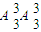
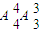
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com