
| A. | $\sqrt{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | -$\sqrt{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
分析 先找二面角A1-BD-A的平面角,在△A1OA中,∠A1OA即为二面角A1-BD-A的平面角.根据二面角A1-BD-C与二面角A1-BD-A 互为补角进行求解即可.
解答 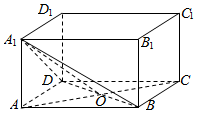 解:连接AC交BD与点O如图所示,
解:连接AC交BD与点O如图所示,
因为AA1⊥BD,AC⊥BD,
所以∠A1OA即为二面角A1-BD-A的平面角,
∠A1OC即为二面角A1-BD-C的平面角,
且二面角A1-BD-C与二面角A1-BD-A 互为补角,
在△A1OA中,设AA1=a,则AO=$\frac{1}{2}AC=\frac{\sqrt{2}}{2}a$,
所以二面角A1-BD-A的正切值为tan∠A1OA=$\frac{{A}_{1}A}{AO}$=$\frac{a}{\frac{\sqrt{2}}{2}a}=\sqrt{2}$,
∵tan∠A1OC=tan(π-∠A1OA)=-tan∠A1OA=-$\sqrt{2}$,
故选:C
点评 本题主要考查二面角的大小求解,根据二面角的定义,找出二面角的平面角是解决本题的关键.注意由于二面角A1-BD-C是钝二面角根据条件转化为求二面角A1-BD-A进行求解.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
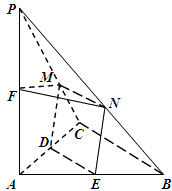 如图,在三棱锥P-ABC中,PA⊥平面ABC,2AC=PC=2,AC⊥BC,F为AP的中点,M、N、D、E分别为线段PC、PB、AC、AB上的动点,且MN∥BC∥DE.
如图,在三棱锥P-ABC中,PA⊥平面ABC,2AC=PC=2,AC⊥BC,F为AP的中点,M、N、D、E分别为线段PC、PB、AC、AB上的动点,且MN∥BC∥DE.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
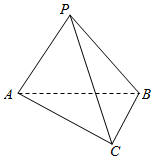 如图,把等腰直角三角形ABC以斜边AB为轴旋转,使C点移动的距离等于AC时停止,并记为点P.
如图,把等腰直角三角形ABC以斜边AB为轴旋转,使C点移动的距离等于AC时停止,并记为点P.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四棱锥P-ABCD的底面是边长为1的正方形,PA⊥底面ABCD,E、F分别为AB、PC的中点.
如图,四棱锥P-ABCD的底面是边长为1的正方形,PA⊥底面ABCD,E、F分别为AB、PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
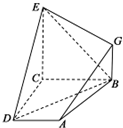 如图,已知四边形ABCD和BCEG均为直角梯形,AD∥BC,CE∥BG,且$∠BCD=∠BCE=\frac{π}{2}$,平面ABCD⊥平面BCEG,BC=CD=CE=2AD=2BG=2
如图,已知四边形ABCD和BCEG均为直角梯形,AD∥BC,CE∥BG,且$∠BCD=∠BCE=\frac{π}{2}$,平面ABCD⊥平面BCEG,BC=CD=CE=2AD=2BG=2查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com